Numerische Methoden zur Lösung von gewöhnlichen Differentialgleichungen: Randwertprobleme.

Das lineare Randwertproblem zweiter Ordnung.

Es ist im Rahmen dieser Lehrveranstaltung völlig unmöglich, das sehr umfangreiche Gebiet der numerischen Behandlung von Randwertproblemen (RWP) umfassend zu behandeln. Ich habe daher aus der großen Mannigfaltigkeit der Probleme jene Gruppe herausgegriffen, die in der Praxis von Physik und Technik die wichtigste Rolle spielt, nämlich

lineare Randwertprobleme zweiter Ordnung mit entkoppelten Randbedingungen.

Dieses Problem besteht in mathematischer Hinsicht aus der gewöhnlichen linearen Differentialgleichung (Dgl.) zweiter Ordnung

$$r(x) y''(x) + s(x) y'(x) + q(x) y(x) = f(x)\qquad (x \in [a,b])$$ (9.1)

mit den in bezug auf die Intervallgrenzen $a$ und $b$ entkoppelten Randbedingungen

$$\alpha_{0} y(a) + \alpha_{1} y'(a) = \gamma\qquad (\vert\alpha_{0}\vert + \vert\alpha_{1}\vert \ne 0)$$ (9.2)

und

$$\beta_{0} y(b) + \beta_{1} y'(b) = \delta\qquad (\vert\beta_{0}\vert + \vert\beta_{1}\vert \ne 0)\quad .$$ (9.3)

Man nennt ein Problem (9.1-9.3) homogen, wenn gilt:

$$f(x)\equiv 0\qquad \gamma=0\qquad \delta=0 .$$

In allen anderen Fällen liegt ein inhomogenes RWP vor.

Numerische Behandlung des inhomogenen RWP mittels des Differenzenverfahrens.

Der wichtigste Schritt beim Differenzenverfahren besteht darin, daß das kontinuierliche Intervall, innerhalb dessen die Lösungsfunktion $y(x)$ gesucht wird, durch Aufteilung in N (gleich-breite) Subintervalle diskretisiert wird. Man erhält auf diese Weise die $N+1$ äquidistanten Stützpunkte

$$x_{i}=a + (i-1)h\qquad \mbox{mit } h=\frac{b-a}{N}\quad\mbox{und } (i=1,\ldots,N+1) .$$ (9.4)

An diesen Stützpunkten werden nun alle in der Dgl. und in den Randbedingungen auftretenden Differentialquotienten durch geeignete Differenzenquotienten ersetzt.

Es gibt nun in der Literatur zahlreiche Formeln für solche Differenzenquotienten (s. z. B. [20], S. 267 und 267). In vielen Fällen sind jedoch die einfachsten derartigen Formeln die numerisch praktikabelsten. Aus diesem Grund werden in diesem Kapitel aussschließlich die sogenannten 'symmetrischen Dreipunktsformeln'^9.1

$$y'_{i}\approx \frac{y_{i+1}-y_{i-1}}{2h}$$ (9.5)

bzw.

$$y''_{i}\approx \frac{y_{i+1}-2y_{i}+y_{i-1}}{h^{2}}$$ (9.6)

verwendet.

Die grafische Interpretation von (9.5) und (9.6) ist besonders einfach: Die Steigung der Kurve im Punkt $x_{i}$ wird approximiert durch die Steigung der Verbindungsgeraden, die durch den rechten und den linken Nachbarpunkt hindurchgeht (s. Abb. 9.1).
Entsprechend wird die zweite Ableitung der Funktion $y(x)$ im Punkt $x_{i}$ durch die zweite Ableitung jener Parabel angenähert, die durch den Punkt $(x_{i},y_{i})$ selbst sowie durch seinen rechten und linken Nachbarn hindurchgeht.

Abbildung 9.1: Grafische Interpretation des finiten Ausdrucks (9.5).

Ersetzt man nun die erste und zweite Ableitung in (9.1) durch die Ausdrücke (9.5) und (9.6), so erhält man für $i=1,\ldots,N+1$ die Differenzengleichungen

$$r_{i}\frac{(y_{i+1}-2y_{i}+y_{i-1})}{h^{2}} + s_{i}\frac{(y_{i+1}-y_{i-1})}{2h} + q_{i}y_{i} = f_{i}$$

bzw.

$$\left(\frac{r_{i}}{h^{2}}-\frac{s_{i}}{2h}\right) y_{i-1} + ... ...\frac{r_{i}}{h^{2}}+\frac{s_{i}}{2h}\right) y_{i+1} = f_{i} .$$ (9.7)

Dieses System von Differenzengleichungen bildet ein lineares, inhomogenes Gleichungssystem für die unbekannten Funktionswerte der Lösungsfunktion des RWP. an den $N+1$ Stützpunkten.
Allerdings ist das System (9.7) noch unterbestimmt, denn es enthält (in der ersten Gleichung) die Unbekannte $y_{0}$ sowie (in der $(N+1)$ten Gleichung) die Unbekannte $y_{N+2}$. Diese beiden Größen können, wie gleich gezeigt wird, mittels der beiden Randbedingungen (9.2) und (9.3) aus dem System eliminiert werden.

Einbeziehung der ersten Randbedingung:

Diese Randbedingung beschreibt das Verhalten der Lösungsfunktion an der Stelle $x=a$ d.h. für $i=1$:

$$y(a)\equiv y_{1}\qquad\mbox{und}\qquad y'(a)\equiv y'_{1}\approx \frac{y_{2}-y_{0}}{2h}$$

bzw.

$$\alpha_{0} y_{1} + \alpha_{1} \frac{y_{2}-y_{0}}{2h} = \gamma .$$

Diese Gleichung wird nach $y_{0}$ aufgelöst, und man erhält unter der Voraussetzung $\alpha_{1} \ne 0$

$$y_{0}=\frac{1}{\alpha_{1}}\left( 2h\alpha_{0} y_{1} + \alpha_{1} y_{2} - 2h\gamma\right) .$$ (9.8)

$y_{0}$ setzt man in die erste Differenzengleichung von (9.7) ein, also in die Gleichung

$$\left(\frac{r_{1}}{h^{2}}-\frac{s_{1}}{2h}\right) y_{0} + ... ...(\frac{r_{1}}{h^{2}}+\frac{s_{1}}{2h}\right) y_{2} = f_{1} .$$

Dies ergibt die neue erste Differenzengleichung

$$\left[ q_{1}-\frac{2 r_{1}}{h^{2}} -\frac{\alpha_{0}}{\alpha... ...ac{\gamma}{\alpha_{1}}\left( s_{1}-\frac{2 r_{1}}{h}\right) .$$ (9.9)

Dies gilt, wie bereits gesagt, für $\alpha_{1} \ne 0$. Im Falle $\alpha_{1}=0$ ergibt sich direkt aus der ersten Randbedingung die Gleichung

$$y_{1} = \frac{\gamma}{\alpha_{0}} .$$ (9.10)

Einbeziehung der zweiten Randbedingung:

Die Behandlung der Randbedingung (9.3) geschieht äquivalent zu den obigen Überlegungen und führt unter der Bedingung $\beta_{1}\ne 0$ zur folgenden neuen letzten (d. h. ($N+1$)-ten) Differenzengleichung

$$\frac{2 r_{N+1}}{h^{2}} y_{N} + \left[ q_{N+1} - \frac{2 r_{... ...elta}{\beta_{1}}\left( s_{N+1} +\frac{2 r_{N+1}}{h}\right) .$$ (9.11)

Im Falle $\beta_1=0$ ergibt sich aus (9.3) sofort

$$y_{N+1} = \frac{\delta}{\beta_{0}} .$$ (9.12)

Auf diese Weise hat man das gegebene RWP in ein inhomogenes, lineares Gleichungssystem von $N+1$ Gleichungen für die $N+1$ Unbekannten $y_{1}, y_{2},\ldots, y_{N+1}$.
Die erste Gleichung dieses Systems ist gegeben durch (9.9) bzw. (9.10), die zweite bis $N$-te Gleichung hat die Form (9.7), und die ($N+1$)-te Gleichung lautet (9.11) bzw. (9.12).

Wie bereits erwähnt, stellen die Lösungen dieses Systems die approximativen Werte der Lösungsfunktion $y(x)$ des RWP an den Stützpunkten $x_{1}\ldots x_{N+1}$ dar. Dieses System muß also (i. a. mit numerischen Mitteln) gelöst werden.
Eine Analyse der Differenzengleichungen zeigt Ihnen sofort, daß die Koeffizientenmatrix des linearen Gleichungssystems eine tridiagonale Matrix ist. Diese einfache Form ist der speziellen Wahl der finiten Elemente (9.5) und (9.6) zu danken!

Wie Sie sich erinnern, gibt es für die Lösung von linearen Gleichungssystemen mit tridiagonaler Matrix sehr effizente numerische Methoden. Eine solche finden Sie im Abschnitt 2.6.1 dieses Skriptums.

Fehlerdiagnostik und Fehlerkorrektur.

Wiederholt man die Berechnung der $y_{i}$ mit der doppelten Zahl von Subintervallen (d.h.: $N\rightarrow 2N$), so entspricht wegen der äquidistanten Stützpunkte jeder zweite Punkt der '2$N$-Rechnung' einem Punkt der '$N$-Rechnung'. Für diese Punkte kann man nun eine sehr einfache und äquidistante Reduktion des beim Differenzenverfahren auftretenden Verfahrensfehlers vornehmen; diese Methode beruht auf dem in der Literatur beschriebenen Faktum, daß der Verfahrensfehler für $y_{i}$ die Form

$$E_{V} = \frac{C(N)}{N^{2}}$$ (9.13)

hat. Der (unbekannte) exakte Wert von $y_{i}$ kann also in der Form

$$y_{i,exakt} = \hat y_{i}(N) + \frac{C_{i}(N)}{N^{2}}$$

geschrieben werden, wobei $\hat y(N)$ den mittels des Differenzenverfahrens ($N$ Subintervalle) erhaltenen Näherungswert bedeutet.
Verdoppelt man die Anzahl der Subintervalle, so ergibt sich

$$y_{i,exakt} = \hat y_{i}(2N) + \frac{C_{i}(2N)}{(2N)^{2}} .$$

Wie im ganz ähnlichen Fall der Fehlerabschätzung beim Runga-Kutta-Verfahren (s. Abschnitt 8.4.5), macht man auch hier die Approximation

$$C_{i}(N)\approx C_{i}(2N) = C_{i}$$

und man erhält sofort

$$C_{i} = \frac{4N^{2}}{3}\left[ \hat y_{i}(2N) - \hat y_{i}(N)\right]$$

bzw. die Korrekturformel

$$y_{i,korr} = \frac{4\hat y_{i}(2N) - \hat y_{i}(N)}{3} .$$ (9.14)

Die Leistungsfähigkeit dieser Formel wird in den folgenden Testbeispielen demonstriert.

Das Programm DIFF1.

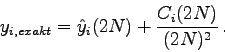
Dieses Programm löst das RWP (9.1)-(9.3) mittels des Differenzenverfahrens. Die Hauptpunkte des Programmes sind:

1. Berechnung der Funktionswerte von $r(x)$, $s(x)$, $q(x)$ und $f(x)$ für die Stützpunkte $x_{i}=a+(i-1)h$ mit $h=(b-a)/N$ und $i=1,\ldots,N+1$ mittels der Prozedur FCT1.
2. Berechnung der 3 Vektoren ${\bf a}, {\bf b}, {\bf c}$ der tridiagonalen Matrix sowie des inhomogenen Vektors gemäß den Gleichungen (9.9; 9.10), (9.7) und (9.11;9.12).
   Achtung auf die Sonderfälle $\alpha_{1}=0$ und/oder $\beta_{1}=0$.
3. Aufruf des Programmes TRID (s. Abschnitt 2.6.1). Der Lösungsvektor ${\bf y}$ stellt die Näherungen der Lösungsfunktion $y(x)$ des RWP an den Stützpunkten $x_{i}$ dar.
4. Die Schritte (1)-(3) werden zweimal durchgeführt, einmal mit der gewählten Intervallanzahl $N$, und ein zweitesmal mit der Intervallanzahl $2N$.
5. Die entsprechenden $\hat y$-Werte werden mittels der Fehlerkorrekturformel (9.14) verbessert.

INPUT-Parameter:

ANF, AEND:

$a$ und $b$ in (9.1).

ALP0,ALP1,BET0,BET1:

Parameter der entkoppelten Randbedingungen (9.2) und (9.3).

GAMMA, DELTA:

inhomogene Parameter in (9.2) und (9.3).

N0:

Anzahl der Subintervalle für den ersten Durchlauf in DIFF1.

OUTPUT-Parameter:

Y():

eindim. Feld mit den Näherungswerten der Lösungsfunktion $y(x)$ an den Stützpunkten im Intervall [$a$,$b$].

INTERNE FELDER:

YY(,):

zweidim. Feld mit den Näherungswerten der Lösungsfunktion $y(x)$ für $N$ und $2N$ Subintervalle.

Das Programm DIFF1 benötigt die Prozeduren FCT1 und TRID.

=16cm Struktogramm 29DIFF1(ANF,AEND,ALP0,ALP1,BET0,BET1,GAMMA,
DELTA,N0,Y)T=1(1)2N:=T*N0
H:=(AEND-ANF)/N
HQ:=H*HI=2(1)N X:=ANF+(I-1)*H FCT1(X,R,S,Q,F) A(I):=R/HQ-S/2.0/H
B(I):=Q-2.0*R/HQ
C(I):=R/HQ+S/2.0/H
INHOM(I):=FALP1=0.0B(1):=1.0
C(1):=0.0
INHOM(1):=GAMMA/ALP0 FCT1(ANF,R,S,Q,F)B(1):=Q-2.0*R/HQ - ALP0/ALP1*(S-2.0*R/H)
C(1):=2.0*R/HQ
INHOM(1):=F - GAMMA/ALP1*(S-2.0*R/H)BET1=0.0A(N+1):=0.0
B(N+1):=1.0
INHOM(N+1):=DELTA/BET0 FCT1(AEND,R,S,Q,F)A(N+1):=2.0*R/HQ
B(N+1):=Q-2.0*R/HQ - BET0/BET1*(S+2.0*R/H)
INHOM(N+1):=F - DELTA/BET1*(S+2.0*R/H) NP1:=N+1TRID(A,B,C,INHOM,NP1,Y) I=1(1)N0+1T=1 INDEX:=IINDEX:=2*I-1 YY(I,T):=Y(INDEX) H:=(AEND-ANF)/N0 I=1(1)N0+1 X:=ANF+(I-1)*H
Y(I):=(4.0*YY(I,2)-YY(I,1))/3.0(return)

Ein Testbeispiel für DIFF1.

Das nun folgende Beispiel soll Ihnen die Leistungsfähigkeit von DIFF1 demonstrieren. Es ist der Referenz [19], S. 252f entnommen und lautet:

$$y''(x) - 2xy'(x) -2y = -4x \qquad (x\in [0,1])$$

und

$$y(0) - y'(0) =0\qquad \mbox{bzw.}\qquad y(1) = 1+{\rm e} .$$

Die exakte Lösung dieses RWP lautet:

$$y(x)=x + {\rm e}^{x^{2}} .$$

Der Benutzer hat also eine Prozedur FCT1 zu schreiben, welche z. B. die Form hat:

.
PROCEDURE FCT1(x: real; VAR r,s,q,f: real);

BEGIN
  r:=1.0;
  s:=-2.0*x;
  q:=-2.0;
  f:=-4.0*x
END;

Die weiteren Parameter lauten:

.
  anf=0.0    aend=1.0

  alp0=1.0   alp1=-1.0     bet0=1.0   bet1=0.0
        gamma=0.0             delta=1.0 + e

Die Auswertung mittels DIFF1 wurde für N0=10 Subintervalle durchgeführt, d.h. das Programm DIFF1 führte die Rechnung einmal mit 10 Subintervallen und ein zweitesmal mit 20 Subintervallen durch; dann wurde die Korrekturformel (9.14) angewendet.
Die Ergebnisse sehen Sie in den folgenden Tabellen sowie in der Abb. 9.2.

.
Testergebnisse fuer DIFF1: absolute Fehler zwischen Naeherungswerten und
                           exakten Werten:

  x                           abs. Fehler
             n=10                n=20           korr. mittels
                                                     (9.14)

 0.0    1.9162406497E-03    4.7755794913E-04   -2.0029510779E-06
 0.1    2.0768600371E-03    5.1777355657E-04   -1.9219369278E-06
 0.2    2.1803285636E-03    5.4365274082E-04   -1.9058661564E-06
 0.3    2.2261855847E-03    5.5508881815E-04   -1.9434355636E-06
 0.4    2.2088322276E-03    5.5069313748E-04   -2.0198913262E-06
 0.5    2.1176171067E-03    5.2782016428E-04   -2.1121486498E-06
 0.6    1.9371537346E-03    4.8265275109E-04   -2.1809100872E-06
 0.7    1.6485163578E-03    4.1051038716E-04   -2.1582709451E-06
 0.8    1.2326037795E-03    3.0670399065E-04   -1.9292747311E-06
 0.9    6.7823138306E-04    1.6857800802E-04   -1.3064491213E-06
 1.0    1.0913936421E-11    1.0913936421E-11    1.0913936421E-11

Abbildung 9.2: Absolute Fehler der Näherungslösungen des Testbeispiels für DIFF1.

Numerische Behandlung des homogenen RWP mittels des Differenzenverfahrens.

Im folgenden soll nun die numerische Auswertung des homogenen RWP (9.1)-(9.3) diskutiert werden, und zwar in der Form eines Eigenwertproblems:

$$r(x) y''(x) + s(x) y'(x) + q(x) y(x) = \lambda y(x)\qquad (x \in [a,b])$$ (9.15)

mit den Randbedingungen

$$\alpha_{0} y(a) + \alpha_{1} y'(a) = 0\qquad (\vert\alpha_{0}\vert + \vert\alpha_{1}\vert \ne 0)$$ (9.16)

und

$$\beta_{0} y(b) + \beta_{1} y'(b) = 0\qquad (\vert\beta_{0}\vert + \vert\beta_{1}\vert \ne 0)\quad .$$ (9.17)

Für ein solches Problem gibt es immer die triviale Lösung $y(x)\equiv 0$ sowie für bestimmte Werte von $\lambda$ nicht-triviale Lösungen. Man spricht von den Eigenwerten und Eigenfunktionen (Eigenlösungen) des homogenen RWP.

Die mathematische Behandlung von (9.15)-(9.17) ist identisch mit der Vorgangsweise in Abschnitt 9.2. Wieder wird das RWP durch Diskretisierung des Intervalles [$a$,$b$] in ein lineares, diesmal natürlich homogenes Gleichungssystem umgewandelt. Unter der Voraussetzung $\alpha_{1} \ne 0$ und $\beta_{1}\ne 0$ erhält man

$$\left[\underbrace{ q_{1}-\frac{2 r_{1}}{h^{2}} - \frac{\alph... ...1} + \underbrace{\frac{2 r_{1}}{h^{2}}}_{c_{1}} y_{2} = 0 ,$$ (9.18)

für $(i=2,\ldots,N)$

$$\underbrace{\left(\frac{r_{i}}{h^{2}}-\frac{s_{i}}{2h}\right... ...c{r_{i}}{h^{2}}+\frac{s_{i}}{2h}\right)}_{c_{i}} y_{i+1} = 0$$ (9.19)

und

$$\underbrace{\frac{2 r_{N+1}}{h^{2}}}_{a_{N+1}} y_{N} + \l... ... r_{N+1}}{h}\right)}_{b_{N+1}} - \lambda\right] y_{N+1} =0 .$$ (9.20)

Auf diese Weise hat man das Eigenwertproblem des RWP in das Eigenwertproblem einer tridiagonalen Matrix umgewandelt:

$$\left( \begin{array}{ccccc} b_{1}-\lambda & c_{1} &&& \\ a_... ...{2} . . . y_{N} y_{N+1} \end{array} \right) = 0 .$$ (9.21)

Das Auftreten von $\alpha_{1}=0$ und/oder $\beta_{1}=0$ bedeutet eine harmlose Komplikation: in diesem Fall gehen die Randbedingungen (9.16) und/oder (9.17) in die simple Form

$$y(a)\equiv y_{1}=0\qquad\mbox{und/oder}\qquad y(b)\equiv y_{N+1}=0$$

über, d. h., daß die erste und/oder letzte Komponente des Lösungsvektors bereits feststeht und daher in (9.21) nicht mehr als Unbekannte aufscheinen muß.
In einem solchen Fall muß die Koeffizientenmatrix in (9.21) um die erste und/oder letzte Zeile und Spalte verjüngt werden! Wie dies im Detail geschieht, können Sie dem Struktogramm Nr. 30 entnehmen.

In jedem Fall hat man nun die Eigenwerte einer tridiagonalen Matrix zu ermitteln. Dies kann z. B. mittels des Hyman-Verfahrens in Zusammenarbeit mit einem Nullstellen-Suchprogramm wie INTSCH geschehen. Genaueres zu diesem Thema finden Sie im Abschnitt 7.5.5 dieses Skriptums.

Fehlerkorrektur der Eigenwerte.

Ohne weitere theoretische Ableitungen soll hier eine Formel für die Fehlerkorrektur der so erhaltenen Näherungen der Eigenwerte des RWP angegeben werden. Bezeichnet man mit $\lambda(N)$ bzw. mit $\lambda(2N)$ einen Eigenwert der tridiagonalen Matrix in (9.21), wobei das Intervall $[a,b]$ in $N$ bzw. $2N$ Subintervalle geteilt wurde, so kann der Verfahrensfehler bzgl. dieses Eigenwertes mittels der Formel

$$\lambda_{korr} = \frac{4\lambda(2N)-\lambda(N)}{3}$$ (9.22)

signifikant reduziert werden (vgl. Abschnitt 9.2.1).

Es soll hier aber ein ganz wesentlicher Nachteil dieser Korrekturformel nicht verschwiegen werden: man hat keinerlei Information über die Genauigkeit der korrigierten Eigenwerte!

Das Programm DIFF2.

Dieses Programm berechnet einige reelle Eigenwerte des homogenen RWP (9.15)-(9.17) mittels des Differenzenverfahrens sowie des Verfahrens von
Hyman (s. Abschnitt 7.5.5).
Die Hauptpunkte des Programmes sind:

1. Zählschleife mit T=1(1)2: Um die Korrekturformel (9.22) anwenden zu können, muß die Eigenwertbestimmung zweimal durchgeführt werden, und zwar sowohl mit der gegebenen Subintervallanzahl N0 als auch mit der doppelten Subintervallanzahl.
2. Bestimmung der Funktionswerte der Koeffizientenfunktionen $r(x)$, $s(x)$ und $q(x)$ durch Aufruf der Prozedur FCT1.
3. Berechnung der 3 Vektoren der tridiagonalen Matrix in (9.21) unter Berücksichtigung eines eventuellen Nullwerdens von $\alpha_{1}$ oder/und $\beta_{1}$.
4. Aufruf des Nullstellen-Suchprogrammes INTSCH (Abschnitt 5.5). Dieses Programm ruft die HYMAN-Funktion auf, wobei die drei Vektoren der tridiagonalen Matrix [die Felder A(), B() und C()] zusammen mit der aktuellen Ordnung der Matrix an die Funktion HYMAN übergeben werden müssen, gegebenenfalls durch die Definition globaler Parameter (Details zum Zusammenwirken von HYMAN und INTSCH siehe Abschnitt 7.5.5).
   INTSCH liefert die 'unkorrigierten' Eigenwerte. Die Anzahl der beim ersten bzw. zweiten Durchlauf gefundenen Eigenwerte ist ANZ(1) bzw. ANZ(2). Abspeicherung der unkorrigierten Eigenwerte auf das Feld EWERTE(...,T).
5. Nach dem zweiten Durchlauf (mit doppelter Subintervallanzahl) werden die entsprechenden Eigenwerte mittels (9.22) verbessert. Dabei muß sichergestellt sein, daß nur zusammengehörende Eigenwerte in die Formel (9.22) eingesetzt werden. Um dies mit ausreichender Sicherheit zu gewährleisten, wird vor der Fehlerkorrektur abgefragt, ob in beiden Rechendurchläufen dieselbe Zahl von Eigenwerten eruiert wurde. Ist dies nicht der Fall, Fehleranzeige und Return.

INPUT-Parameter:

ANF,AEND:

$a$ und $b$ in (9.15).

ALP0,ALP1,BET0,BET1:

Parameter $\alpha_{0}$, $\alpha_{1}$, $\beta_{0}$ und $\beta_{1}$ in den Randbedingungen (9.16) und (9.17).

Die folgenden 4 Input-Parameter beziehen sich auf die von DIFF2 aufgerufene Prozedur INTSCH:

ANFEIG,ENDEIG:

Anfang und Ende des Grobsuchbereiches für die Eigenwerte.

HEIG:

Schrittweite für die Eigenwertsuche.

GENEIG:

Fehlerschranke für die von INTSCH ermittelten Eigenwerte.

N0:

Anzahl der Subintervalle für den ersten Durchlauf von DIFF2.

OUTPUT-Parameter:

ANZEIG:

Zahl der ermittelten (korrigierten) Eigenwerte.

EIGW( ):

Feld der ermittelten (korrigierten) Eigenwerte.

FEHL1:

(logische) Fehlerdiagnostik-Variable:
$\qquad$ FEHL1=TRUE: Eigenwert-Korrektur war nicht möglich;
$\qquad$ FEHL1=FALSE: Eigenwert-Korrektur ok.

INTERNE FELDER:

EWERTE(,):

zweidimensionales Feld mit den unkorrigierten Eigenwerten für N0 bzw. 2N0 Subintervalle.

Das Programm DIFF2 benötigt die Prozeduren FCT1, INTSCH
und HYMAN.

Anmerkung:
Um die Verfahrensfehler von INTSCH möglichst klein zu halten, sollte die Fehlerschranke GENEIG sehr klein gewählt werden,
z.B.:    GEN = 0.0000001.
Um dieser Anforderung gerecht zu werden, sollte DIFF2 - wenn möglich - mit doppelter Genauigkeit gerechnet werden.

=16cm Struktogramm 30DIFF2(ANF,AEND,ALP0,ALP1,BET0,BET1,ANFEIG,
ENDEIG,HEIG,GENEIG,N0,ANZEIG,EIGW,FEHL1)T=1(1)2N:=T*N0
H:=(AEND-ANF)/N
HQ:=H*HI=2(1)N X:=ANF+(I-1)*H FCT1(X,R,S,Q) A(I):=R/HQ-S/2.0/H
B(I):=Q-2.0*R/HQ
C(I):=R/HQ+S/2.0/HALP1=0.0IANF:=2IANF:=1 FCT1(ANF,R,S,Q)B(1):=Q-2.0*R/HQ - ALP0/ALP1*(S-2.0*R/H)
C(1):=2.0*R/HQBET1=0.0IEND:=NIEND:=N+1 FCT1(AEND,R,S,Q)A(N+1):=2.0*R/HQ
B(N+1):=Q-2.0*R/HQ - BET0/BET1*(S+2.0*R/H)N:=IEND-IANF+1ALP1=0.0I=1(1)NA(I):=A(I+1)
B(I):=B(I+1)
C(I):=C(I+1)......INTSCH(ANFEIG,ENDEIG,HEIG,GENEIG,ANZMAX,EIGW,ANZ(T))ANZ(T)=0print: DIFF2 'keine Nullst. in INTSCH'I=1(1)ANZ(T)EWERTE(I,T):=EIGW(I) ANZEIG:=ANZ(2)ANZ(1)=ANZ(2)I=1(1)ANZEIG EIGW(I):=(4.0*EWERTE(I,2) - EWERTE(I,1))/3.0 FEHL1:=FALSEprint: DIFF2 'Keine Korrektur'I=1(1)ANZEIGEIGW(I):=EWERTE(I,2)FEHL1:=TRUE(return)

Ein Testbeispiel für DIFF2.

Als Test für die Leistungsfähigkeit des eben besprochenen Algorithmus soll nun das lineare, homogene EWP zweiter Ordnung

$$-y''(\vartheta) - \frac{\cos\vartheta}{\sin\vartheta} y'(\vartheta) = \lambda y(\vartheta)$$

$$.$$ (9.23)

$$y(\pi/2)=0 \qquad \qquad y'(\pi)=0$$

mittels DIFF2 ausgewertet werden.

Die Eigenwerte $\lambda$ dieses Problems gehorchen der Formel

$$\lambda_{m} = (2m-1)\cdot 2m \qquad m=1,2,\ldots$$ (9.24)

und die entsprechenden Eigenfunktionen sind die Legendre-Polynome 1. Art mit ungeraden Ordnungen.

Im Bereich $0\leq \lambda \leq 100$ gibt es also die 5 Eigenwerte

$$2 \qquad 12 \qquad 30 \qquad 56 \qquad 90 .$$

Die INPUT-Parameter und die Prozedur FCT1 lauten in diesem Fall:

.
anf:=1.57079633    aend:=3.14159265

alp0:=1.0   alp1:=0.0   bet0:=0.0   bet1:=1.0

n0:=50

anfeig:=0.0    endeig:=100.0    heig:=1.0    geneig:=0.0000001



PROCEDURE FCT1(x: double; VAR r,s,q: double);

BEGIN
  r:=-1.0;
  IF(abs(x-PI) < 1.e-15)THEN s:=0.0 ELSE s:=-cos(x)/sin(x);
  q:=0.0;
END;

Anmerkung zu FCT1:

Bei der Auswertung der Koeffizientenfunktion $s(x)$ ist darauf zu achten, daß sie für $x=\pi$ eine Singularität hat. In der obigen Routine wird $s$ für diesen Fall einfach Null gesetzt. Dies ist aber nur deshalb möglich, weil der in der Dgl. (9.23) vorkommende Term

$$\frac{\cos\vartheta}{\sin\vartheta} y'(\vartheta)$$

für $\vartheta \rightarrow \pi$ nicht divergiert! Die Folge davon ist nämlich (was hier nicht im Detail bewiesen werden soll), daß der dritte Term des in (9.20) definierten Elementes $b_{N+1}$,

$$-\frac{\beta_{0}}{\beta_{1}} \left(s_{N+1} + \frac{2 r_{N+1}}{h}\right) ,$$

für $\beta_{0}=0$ verschwindet.

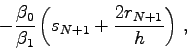
Löst man das vorliegende Problem mit Hilfe der im vorigen Abschnitt präsentierten Prozedur DIFF2, so erhält man das folgende Ergebnis:

.
 Zahl der Subintervalle <=    50
 GENEIG = 0.0000001

          N=50       N=100     korr. nach    exakt
                                (9.22) 

    1    1.99901    1.99975    2.00000         2
    2   11.97850   11.99463   12.00001        12
    3   29.88705   29.97181   30.00006        30
    4   55.64148   55.91053   56.00021        56
    5   89.12707   89.78212   90.00047        90

Die 'shooting method'.

Anschließend soll hier noch die in der Praxis häufig verwendete Methode besprochen werden, das homogene RWP (9.15-9.17) durch Überführung in ein Anfangswertproblem zu lösen.
Zu diesem Zweck bringt man (9.15) in die Form

$$y''(x) = -\frac{s(x)}{r(x)} y'(x) - \frac{\left[ q(x)-\lambda\right]} {r(x)} y(x)$$ (9.25)

für $x\in [a,b]$.

Die Anfangsbedingungen:

Man benötigt für die Dgl. zweiter Ordnung natürlich zwei Anfangsbedingungen. Diese folgen sofort aus der ersten Randbedingung (für $x=a$), welche die Form

$$\alpha_{0} y(a) + \alpha_{1} y'(a) = 0$$

hat. Im Fall $\alpha_{1} \ne 0$ kann man nun für $y(a)$ jede beliebige reelle Zahl (außer Null) setzen. Dies ist möglich, weil die Lösungsfunktion eines homogenen Problems stets nur bis auf eine multiplikative Konstante fixiert ist. Man kann also z. B. einfach festsetzen:

$$y(a) = 1.0 .$$ (9.26)

Der Anfangswert von $y'(x)$ ergibt sich dann sofort als

$$y'(a)=-\frac{\alpha_{0}}{\alpha_{1}} y(a) = -\frac{\alpha_{0}}{\alpha_{1}} .$$ (9.27)

Ist hingegen $\alpha_{1}=0$, so bleibt für $y(x)$ nur mehr die Möglichkeit

$$y(a) = 0.0 ,$$ (9.28)

und die Funktion $y'(x)$ kann am Anfangswert jeden beliebigen Wert außer Null annehmen, also z. B.

$$y'(a) = 1.0 .$$ (9.29)

Die Gleichungen (9.25)-(9.29) definieren ein Anfangswertproblem, das z. B. mittels der im Kapitel 8 besprochenen Verfahren gelöst werden kann.

Bestimmung der Eigenwerte:

Die Eigenwerte $\lambda$ sind noch unbekannt. Man kann nun wie folgt vorgehen: Man löst das Cauchy-Problem (9.25)-(9.29) im Intervall $[a,b]$ für ein beliebiges 'Probe'-$\lambda$.

Nun überprüft man, ob die erhaltene Lösungsfunktion $y(x)$ an der Stelle des rechten Randes, also für $x=b$, die zweite Randbedingung (9.17) erfüllt, d.h. ob gilt:

$$\beta_{0} y(b) + \beta_{1} y'(b) = 0 .$$ (9.30)

Wenn dies der Fall ist, ist das gewählte $\lambda$ einer der Eigenwerte des gegebenen RWP, und $y(x)$ ist (eine Näherung) für die zugehörige Eigenfunktion. Wenn die Bedingung (9.30) nicht erfüllt wird (was natürlich i. a. der Fall sein wird), muß die Auswertung des Anfangswertproblems mit einem neuen Probewert für $\lambda$ wiederholt werden.

Abbildung 9.3: Das Grundprinzip der shooting method.

Abb. 9.3 zeigt das Prinzip dieser Methode: $\lambda_{1}$ und $\lambda_{3}$ 'treffen daneben', $\lambda_{2}$ 'trifft' die Randbedingung bei $b$ und stellt daher einen Eigenwert dar. Die Formulierung 'treffen' bzw. 'daneben treffen' ist bewußt gewählt, um Ihnen den Namen dieser Methode (shooting method) klar zu machen.

Die shooting method hat jedoch einen gravierenden Nachteil: um das Eigenwertproblem mit genügender Genauigkeit zu lösen, müssen sehr viele 'Probe'-$\lambda$ verwendet werden d. h. es müssen sehr viele Cauchy-Probleme gelöst werden, was natürlich häufig große Rechenzeiten bedeutet.

Aus diesem Grund wird die shooting method in der Praxis vor allem in Kombination mit einer sehr schnellen und dennoch genauen Lösungsmethode für das Cauchy-Problem kombiniert, die auf Numerov zurückgeht.

Die Numerov-Methode.

Diese Methode ist nur anwendbar, wenn es gelingt, die Dgl. des homogenen RWP auf die Form

$$y''(x) + k(x) y(x) = 0\qquad x\in[a,b]$$ (9.31)

zu bringen. Dies ist für viele wichtige Anwendungsfälle in Physik und Technik möglich. Ein gutes Beispiel ist etwa die eindimensionale, zeitunabhängige (stationäre) Schrödingergleichung, welche bekanntlich die Form

$$\psi''(x) + \frac{2m}{\hbar^{2}}\left[ E - V(x)\right] \psi(x) = 0$$

hat. In diesem Falle wäre die in (9.31) definierte Funktion $k(x)$ also durch

$$k(x) = \frac{2m}{\hbar^{2}}\left[ E - V(x)\right]$$

bzw., bei Verwendung geeigneter Längen- und Energie-Einheiten, durch

$$k(x) = E - V(x)$$ (9.32)

gegeben.

Die Numerov-Methode ist wieder eine Differenzenmethode, d.h. man teilt das gegebene Intervall in $N$ Subintervalle mit den Stützpunkten

$$x_{i}=a + (i-1)h\qquad (i=1,\ldots,N+1)\qquad\mbox{mit }\quad h=\frac{b-a}{N} .$$

Der nächste Schritt ist eine Taylorreihenentwicklung der Funktion $y(x)$ an der Stelle $x_{i}$ für die Werte $x_{i}\pm h$:

$$y(x_{i}\pm h) \equiv y_{i\pm1} = y_{i} \pm h y'_{i} + \fr... ...{6} y_{i}^{(3)} + \frac{h^{4}}{24} y_{i}^{(4)} \pm \cdots$$

Daraus folgt sofort

$$y_{i+1} + y_{i-1} = 2y_{i} + h^{2} y''_{i} +\frac{h^{4}}{12} y_{i}^{(4)} + \cdots$$ (9.33)

Für $y''_{i}$ kann man nun gemäß (9.31) setzen:

$$y''_{i} = -k_{i} y_{i} .$$ (9.34)

Nun kommt der entscheidende Trick: man diskretisiert die vierte Ableitung von $y(x)$ an der Stelle $x_{i}$ mittels des finiten Elementes (9.6) und erhält mit (9.34)

$$y_{i}^{(4)} \approx \frac{y''_{i+1} - 2y''_{i} + y''_{i-1}}{... ...\frac{2k_{i}y_{i} - k_{i+1}y_{i+1} - k_{i-1}y_{i-1}}{h^{2}} .$$ (9.35)

Setzt man nun (9.34) und (9.35) in die Glg. (9.33) ein und löst diese Gleichung nach $y_{i+1}$ auf, ergibt sich die folgende Rekursionsformel von Numerov:

$$y_{i}\approx \frac{ 2\left(1-\frac{5h^{2}}{12}k_{i-1}\right)... ...} - \frac{h^{2}}{12}k_{i-2}y_{i-2}} {1+\frac{h^{2}}{12} k_{i}}$$ (9.36)

für $i=3,\ldots,N$, wobei die Werte $k_i$ die Funktionswerte von $k(x)$ [Glg. (9.32)] an den Stützpunkten $x_i$ bedeuten:

$$k_i\equiv k(x_i) = E - V(x_i)\qquad\mbox{mit}\quad i=1,\ldots,N+1 .$$ (9.37)

Nun noch einige wichtige Anmerkungen zum shooting-Numerov-Verfahren:

Als ersten Schritt des Numerov-Prozesses muß die Glg. (9.36) für $i=3$ ausgewertet werden. Dies führt zur Formel

$$y_{3}\approx \frac{ 2\left(1-\frac{5h^{2}}{12}k_{2}\right)y_... ...y_1-\frac{h^{2}}{12}k_{1} y_{1}} {1+\frac{h^{2}}{12} k_{3}} .$$ (9.38)

• Um den Numerov-Prozess starten zu können, muß man also die Werte $y_{1}\equiv y(a)$ und $y_{2}\equiv y(a+h)$ kennen. Diese Größen lassen sich gewöhnlich aus den Nebenbedingungen des Problems eruieren.
• In der obigen Formel für $y_3$ kommt die Größe $k_1 = E-V(a)$ vor. Man braucht also den Wert der Potentialfunktion am linken Rand $a$ des Integrationsintervalls. In vielen konkreten Fällen - z.B. wenn $V(x)$ ein Coulomb-Potential ist - hat diese Funktion für $x=a$ eine Singularität und kann daher dort nicht ausgewertet werden.
  Dann kann man oft wie folgt vorgehen: man schreibt die Glg. (9.38) in der Form
  
  $$y_{3}\approx \frac{ 2\left(1-\frac{5h^{2}}{12}k_{2}\right)... ...left[E y_1 - V(x_1)y_{1}\right]} {1+\frac{h^{2}}{12} k_{3}}$$
  
  
  und berechnet analytisch den Grenzwert
  
  $$\mbox{V1Y1} = \lim_{x\to a} V(x)y(x) .$$
  
  
  Beispiele für ein solches Vorgehen finden Sie im Abschnitt 9.4.3 sowie in der Übungsbeschreibung.
• Wie aus den obigen Erläuterungen hervorgeht, muß für eine numerische Berechnung der Eigenwerte der Numerov-Prozess in der Regel sehr oft durchlaufen werden, wobei sich die verwendeten Werte von $k_i$ nur durch einen neuen trial value für $E$ unterscheiden, während die Potentialwerte $V(x_i)$ unverändert bleiben.

  Es wäre nun ausgesprochen ungeschickt, bei jedem Aufruf des Numerov-Programms die Potentialwerte $V(x_i)$ aufs Neue zu berechnen, denn wenn die Potentialfunktion kompliziert ist, würde das eine Menge Rechenzeit kosten. Viel besser ist es, das Feld der Werte $V(x_2)$, $V(x_3)$, ..., $V(x_{N+1}$ vor dem ersten Numerov-Aufruf ein für alle Mal zu berechnen und dieses Feld über die Parameterliste an Numerov zu übergeben. Eine solche Vorgangsweise ist in der folgenden Beschreibung des Numerov-Programms berücksichtigt.

Das Programm NUMEROV.

Die Prozedur NUMEROV führt eine numerische Integration der Dgl. (9.31) durch, wobei diese Gleichung den Eigenwert-Parameter $\lambda$ enthält.

INPUT-Parameter:

ANF,AEND:

$a$ und $b$ in (9.31).

Y1,Y2:

Werte für $y(a)$ und $y(a+h)$.

V1Y1:

Wert für $V(a)y(a)$ (s. dazu die Erläuterungen im vorigen bzw. im Abschnitt 9.4.3).

EIGW:

Probewert für den Eigenwert (shooting method!).

POT:

Vektorfeld mit den Potentialwerten $POT(2)=V(x_2)$, $POT(3)=V(x_3)$, ..., $POT(N+1)=V(x_{N+1})$.

N:

Anzahl der Subintervalle in $[a,b]$.

OUTPUT-Parameter:

YF():

Näherungswerte der Lösungsfunktion $y(x)$ an den Stützpunkten
$x_{1}, x_{2},\ldots, x_{N+1}$.

=14cm Struktogramm 31NUMEROV(ANF,AEND,Y1,Y2,V1Y1,EIGW,POTF,N,YF) H:=(AEND-ANF)/N
HH12:=H*H/12.0 YF(1):=Y1
YF(2):=Y2
YLL:=Y1
YL:=Y2
KL:=EIGW-POTF(2)
K:=EIGW-POTF(3) Y:=(2.0*(1.0-5.0*HH12*KL)*YL - YLL - HH12*(EIGW*YLL-V1Y1)) / (1.0+HH12*K) YF(3):=YI=4(1)N+1YLL:=YL
YL:=Y
KLL:=KL
KL:=K
K:=EIGW-POTF(I) Y:=(2.0*(1.0-5.0*HH12*KL)*YL - YLL - HH12*KLL*YLL) / (1.0+HH12*K) YF(I):=Y(return)

Testbeispiel für die shooting-Numerov-Methode.

Im folgenden soll nun diese Methode auf ein Problem der Metallphysik angewendet werden. Gesucht ist die Grundzustandsenergie und die entsprechende Wellenfunktion eines Valenzelektrons in metallischem Natrium in der Wigner-Seitz-Näherung.

Die Wigner-Seitz-Näherung besteht darin, daß man die i. a. geometrisch recht komplizierte Form der Einheitszelle des Kristalls durch eine volumsgleiche Kugel mit dem Radius $r_{WS}$ ersetzt. Innerhalb der Kugel wird das Kristallpotential durch ein radialsymmetrisches Potential angenähert:

$$V({\bf r})\approx V(r)\qquad \mbox{f\uml ur } r\in [0,r_{WS}] .$$

Unter diesen Umständen sind die Energieeigenwerte $E$ und die Eigenfunktionen eines quantenmechanischen Teilchens (Elektron) durch die stationäre Schrödingergleichung

$$y''(r) + \left\{\frac{2m}{\hbar^{2}}\left[ E - V(r)\right] - \frac{\ell(\ell+1)}{r^{2}}\right\} y(r) = 0$$

gegeben, wobei $y(r)$ der mit $r$ multiplizierte Radialteil der Wellenfunktion des Elektrons ist. Der Parameter $\ell$ stellt die Bahndrehimpuls-Quantenzahl dar; im Falle der Natrium-Valenzelektronen gilt $\ell=0$.

In atomaren Einheiten (Längen in Bohr, Energien in Rydberg) gilt außerdem $2m/\hbar^{2}=1$, und man erhält

$$y''(r) + k(r) y(r) = 0\qquad \mbox{mit}\qquad k(r)=E-V(r)$$ (9.39)

für $r\in [0,r_{WS}]$.

Der Wigner-Seitz-Radius für das Natrium-Metall beträgt 3.9405 Bohr, und als Potential innerhalb der WS-Zelle verwendeten Wigner und Seitz in ihrer Originalarbeit das im folgenden angegebene Prokofjew-Potential:

$$V(r)=-\frac{2Q(r)}{r^{2}}$$ (9.40)

mit

$$Q(r) = \left\{ \begin{array}{cc} 11r & 0\leq r \leq 0.01 ... ... r \leq 6.74 \\ r & 6.74 \leq r < \infty \end{array} \right.$$ (9.41)

.
FUNCTION POT(r: double): double;
VAR
  q : double;
BEGIN
  IF(r <= 0.01)THEN q:=11.0*r
  ELSE IF(r <= 0.15)THEN q:=-26.4*r*r+11.53*r-0.00264
  ELSE IF(r <= 1.00)THEN q:=-2.84*r*r+4.46*r+0.5275
  ELSE IF(r <= 1.55)THEN q:=1.508*r*r-4.236*r+4.876
  ELSE IF(r <= 3.30)THEN q:=0.1196*r*r+0.2072*r+1.319
  ELSE IF(r <= 6.74)THEN q:=0.0005*r*r+0.9933*r+0.0222
  ELSE q:=r;
  pot:=-2.0*q/r/r
END;

Die Randbedingungen:

Die Bedingungen, die eine Eigenfunktion $y(r)$ von (9.39) erfüllen muß, sind die folgenden:

• In der Nähe des linken Randpunktes (d. h. für $r«1$) ist das Kristallpotential $V(r)$ praktisch identisch mit den Coulomb-Potential des Atomkerns mit der Ladungszahl $Z$ (für unser Beispiel Natrium ist $Z=11$). Das heißt, für den Bereich $r«1$ kann die Dgl. (9.39) als
  
  $$y''(r) + \left(E+\frac{2Z}{r}\right) y(r) = 0$$
  
  
  geschrieben werden. Die Lösung dieses Problems hat für kleine $r$ die einfache Form
  
  $$y(r)\propto r .$$
  
  
  Aus diesem Verhalten ergeben sich sofort die Startwerte für die Numerov-Rekursion, nämlich
  
  $$y_{1}=0\qquad\mbox{und}\qquad y_{2}=h .$$
  
  

  
  

  Nun noch ein wichtiges Detail:
  Die Funktion $V(r)$ in (9.39) divergiert offenbar für $r=0$ wegen
  

  $$V(r)=-\frac{2Z}{r}\qquad\mbox{f\uml ur}\quad r\to 0 .$$
  
  
  Das Produkt aus den Funktionen $V(r)$ und $y(r)$ bleibt jedoch auch für $r=0$ beschränkt und ergibt
  
  $$\lim_{r\to 0} V(r)y(r) = -2Z .$$
  
  
  Dieser Wert ist unter dem Namen V1Y1 an die Prozedur NUMEROV zu übergeben (s. Abschnitt 9.4.2).
• Nun wird die shooting method angewendet, d. h. es wird die Variable $\lambda$ solange variiert, bis die mittels NUMEROV erhaltene Funktion $y(x)$ auch die zweite Randbedingung an der rechten Grenze $b$ (im konkreten Fall also für $r=r_{WS}$) erfüllt.
  Die Randbedingung, welcher die Eigenfunktion des Valenzelektrons an der Oberfläche der Wigner-Seitz-Kugel genügen muß, ist die in der Theoretischen Festkörperphysik wohlbekannte Bloch-Bedingung
  
  $$y(r_{WS}) - r_{WS} y'(r_{WS}) \stackrel != 0 .$$
  
  
  Überträgt man diese Bedingung in die entsprechende Differenzengleichung, so ergibt sich die Bedingung
  

  $$y_{N+1} - b\frac{(y_{N+2}-y_{N})}{2h} \stackrel != 0.0 .$$ (9.42)

  
  
  Die Inputgröße EIGW ist also solange zu variieren, bis (9.42) erfüllt wird.

  Anmerkung:    wie Sie sehen, braucht man zur Auswertung der Glg. (9.42) noch den Wert $y_{N+2}$ rechts neben dem Ende des eigentlichen Integrationsintervalls. Um diesen Wert zu erhalten, müssen Sie im Programm Numerov die Zählschleife von I=4(1)N+1 auf I=4(1)N+2 erweitern, und auch die Felder POTF und YF müssen dementsprechend um 1 Speicherplatz erweitert werden.

  
  

  Die folgende Tabelle zeigt die 'Grobsuche' für das konkrete Problem:

  .
  TESTRECHNUNG   SHOOTING-NUMEROV  1999
  
  Wigner-Seitz-Radius [Bohr] = 3.9405
  Zahl der Subintervalle =  400
  
    eigw        y(b)       b*y`(b)      diff (soll Null sein!)
  
  -0.7500      0.3844      0.6288     -0.2444
  -0.6500      0.3259      0.3886     -0.0627
  -0.6400      0.3203      0.3664     -0.0461
  -0.6300      0.3147      0.3445     -0.0298
  -0.6200      0.3092      0.3229     -0.0138
  -0.6100      0.3037      0.3017      0.0020
  -0.6000      0.2982      0.2808      0.0175
  -0.5900      0.2928      0.2601      0.0327
  -0.5800      0.2875      0.2398      0.0476
  -0.5700      0.2821      0.2198      0.0623
  -0.5600      0.2769      0.2002      0.0767
  -0.5500      0.2716      0.1808      0.0908
  -0.4500      0.2215      0.0036      0.2179
  

  Der gesuchte Energie-Eigenwert $E$ für das Natrium-Valenzelektron liegt also im Bereich zwischen -0.62 und -0.61 Rydberg. Eine genauere Rechnung führt zum Ergebnis
  

  $$E = -0.611277\quad \mbox{Rydberg} .$$
  
  
  Die Abb. 9.4 zeigt die entsprechende (unnormierte) Eigenfunktion y(x).

Abbildung 9.4: Ein Ergebnis der shooting-Numerov-Methode: die Eigenfunktion eines Valenzelektrons im Natrium-Kristall (400 Subintervalle im Intervall $[0,r_{WS}]$ mit $r_{ws}$=3.9405 Bohr).
Die Eigenenergie beträgt $-0.611277$ Rydberg.

Software-Angebot

In bezug auf Randwertprobleme gewöhnlicher Differentialgleichungen hat die NAG-Bibliothek einiges zu bieten, wie die folgende Tabelle zeigt:

Sie finden in dieser Tabelle bekannte Begriffe wie shooting method und finite-difference method, wobei die Differenzenmethode nicht nur auf lineare, sondern auch auch nicht-lineare RWP angewendet werden kann. Die Kollokationsmethode nach Chebyshev ist für lineare Probleme ebenfalls sehr leistumgsfähig; es handelt sich dabei um eine Entwicklung der Lösungsfunktion nach Chebyshev-Polynomen und um eine numerische Berechnung der Polynom-Koeffizienten.

Obwohl in dieser LV. die Besprechung der numerischen Behandlung von partiellen Differentialgleichungen (leider) keinen Platz hat, möchte ich abschließend zumindest einige Hinweise auf das sehr umfangreiche Software-Angebot in bezug auf diese Probleme geben:
Einen sehr guten Überblick über p.d. und kommerizielle Software finden Sie in den schon häufig zitierten Büchern von Ch. Überhuber ([21],[22]). So ist z. B. in [21], S. 331ff eine Fallstudie 'Software für elliptische partielle Differentialgleichungen' enthalten, die einschlägige Programme aus den (p.d.) Bibliotheken ELLPACK und TOMS sowie aus NAG und IMSL vorstellt.