Nächste Seite: Numerische Methoden zur Lösung Aufwärts: Numerische Methoden in der Vorherige Seite: Numerische Methoden in der
Die Lehrveranstaltung Numerische Methoden in der Physik beschäftigt sich mit der Lösung physikalisch-technischer Probleme unter Verwendung von Methoden der Numerischen Mathematik, wobei die Komplexizität der Problemstellungen den Einsatz eines Computers erforderlich macht.
Eine Definition des Begriffes Numerische Mathematik findet sich z.B. in [1], S.8:
Die Numerische Mathematik befaßt sich mit der Lösung von mathematischen Problemen mit Hilfe zahlenmäßigen Rechnens. Darunter ist eine endliche Folge von Grundrechenoperationen, also Addition, Subtraktion, Multiplikation und Division zu verstehen, wobei Zahlen mit einer beschränkten Stellenanzahl verwendet werden.
Ebenfalls in [1] ist die grundsätzliche Methodik der Numerischen Mathematik zusammen mit den unvermeidlich auftretenden Fehlern schematisch dargestellt:
|--------------------| |------------------------------|
| Eingabeinformation | ===> | Eingabefehler |
| (Input) | | (Messfehler; Rundungsfehler) |
|--------------------| |------------------------------|
| |
| |
|--------------------| |------------------------------------|
| Algorithmus | ===> | Algorithmusfehler |
| | | (Verfahrensfehler; Rundungsfehler) |
|--------------------| |------------------------------------|
| |
| |
|--------------------| |------------------------------|
| Ausgabeinformation | ===> | Ausgabefehler |
| (Output) | | (Rundungsfehler) |
|--------------------| |------------------------------|
Ein zentraler Begriff der Numerischen Mathematik ist der Begriff Algorithmus. Darunter versteht man nach [2], S.9
eine endliche Menge von genau beschriebenen Anweisungen, die mit vorgegebenen Anfangsdaten in bestimmter Reihenfolge nacheinander auszuführen sind, um die Lösung zu ermitteln.
Wie aus dem obigen Diagramm hervorgeht, tragen alle Aktivitäten bei der Durchführung einer numerischen Rechnung (Dateneingabe; eigentlicher Rechenvorgang; Datenausgabe) zum Fehler des Ergebnisses bei. Ursache dafür sind die auftretenden Rundungsfehler und Verfahrensfehler, auf die in den folgenden Kapiteln ausführlich eingegangen wird.
Ergebnisse von Computerberechnungen sind also (bis auf ganz wenige Ausnahmen) fehlerbehaftet, d.h. sie entsprechen nicht exakt den ,,wahren`` Ergebnissen des behandelten Problems.
Es ist daher von entscheidender Wichtigkeit, bei der Arbeit mit einem Computer die auftretenden Fehler unter Kontrolle (d.h. so klein wie irgend möglich) zu halten bzw. die Genauigkeit der erhaltenen Ergebnisse so gut als möglich beurteilen zu können.
Als Literatur zum Thema "Fehler bei der Anwendung numerischer Verfahrenßind die einschlägigen Kapitel aus [7] und [8] sehr zu empfehlen.
Bevor auf die einzelnen Fehlertypen näher eingegangen wird, sollen im folgenden die Begriffe absoluter und relativer Fehler erläutert werden:
Ist ![]() der (unbekannte) wahre Wert eines Rechenergebnisses und
der (unbekannte) wahre Wert eines Rechenergebnisses und ![]() der entsprechende Näherungswert, so nennt man
der entsprechende Näherungswert, so nennt man
In der Praxis wird meistens der relativen Fehlerbetrachtung nach (1.2) der Vorzug gegeben. Der Grund dafür wird im folgenden einfachen Beispiel klar:
| (a) | 0.1 | 0.09 | 0.01 | |
| (b) | 1000.0 | 999.99 | 0.01 |
=8cm
Struktogramm 1Ermittlung der Kenngröße ![]() tau:=1.0
tau:=1.0
walt:=1.0tau:=tau/2.0
wneu:=walt + tauwneu=waltprint: 2*tau
Es leuchtet sofort ein, daß die Näherung (b) weit befriedigender ist als die Näherung (a), obwohl der absolute Fehler in beiden Fällen gleich ist.
Ein weiterer wichtiger Begriff ist die Maschinen-Genauigkeit: Es ist
dies die kleinste (positive) Zahl ![]() , für welche gilt:
, für welche gilt:
Für einen (nicht-existierenden) Super-Rechner, der reelle Zahlen mit
beliebiger Genauigkeit abspeichern kann, erfüllt natürlich jedes ![]() die obige Ungleichung. Für einen realen Computer ist
die obige Ungleichung. Für einen realen Computer ist ![]() jedoch
eine wichtige Kenngröße, die mit dem Algorithmus im Struktogramm 1 leicht
ermittelt werden kann.
jedoch
eine wichtige Kenngröße, die mit dem Algorithmus im Struktogramm 1 leicht
ermittelt werden kann.
Die folgenden Ergebnisse wurden auf einem IBM-PC erhalten (wie alle in diesem
Skriptum enthaltenen Testergebnisse, soferne es nicht ausdrücklich anders
angegeben ist):
| Bytes | Anz. sign. Stellen | ||
| C-float | 4 |
|
7 |
| C-double | 8 |
|
16 |
| F90-real | 4 |
|
7 |
| F90-double prec. | 8 |
|
16 |
| Pascal-single | 4 |
|
7 |
| Pascal-real | 6 |
|
12 |
| Pascal-double | 8 |
|
16 |
| Pascal-extended | 10 |
|
19 |
// C-PROGRAMM ZUR BERECHNUNG DER MASCHINEN-GENAUIGKEIT
#include <iostream.h>
void main()
{
float tau,walt,wneu;
tau=1.0;
walt=1.0;
do {
tau/=2.0;
wneu=walt+tau;
} while (wneu != walt);
cout<<"TAU = "<<2*tau<<"\n";
}
PROGRAM maschin
! F90-Programm zur Berechnung der Maschinen-Genauigkeit
IMPLICIT NONE
REAL tau,walt,wneu
tau=1.0
walt=1.0
DO
tau=tau/2.0
wneu=walt+tau
IF(wneu .EQ. walt)EXIT
END DO
PRINT '(" tau = ",E12.6)',2.0*tau
END PROGRAM maschin
Eingabe- bzw. Input-Fehler (inherent errors) sind Unsicherheiten der eingegebenen Daten, mit welchen der Computer die Berechnung durchführt. Diese Unsicherheiten können verschiedene Ursachen haben, z.B. experimentelle Meßfehler oder Rundungsfehler.
Wenn die Ergebnisse einer Berechnung stark von diesen Eingabefehlern beeinflußt werden, spricht man von einem 'schlecht konditionierten Problem'.
Dazu als Beispiel ein schlecht konditioniertes lineares Gleichungssystem [7], S.97:
Angenommen, die Größe ![]() sei der experimentell ermittelte Wert
sei der experimentell ermittelte Wert
| 25.503 | 2. | 3. |
| 25.502 | 7. | 2. |
| 25.504 | -3. | 4. |
Das obige Gleichungssystem ist also extrem schlecht konditioniert,
und die Ergebnisse sind (bei Annahme einer experimentell bedingten
Unsicherheit von ![]() ) völlig sinnlos!
) völlig sinnlos!
sind Fehler, die bei der Auswertung der Rechenvorschrift geschehen.
Die Ursache dafür sind entweder Rundungsfehler oder
Verfahrensfehler.
Verfahrensfehler entstehen dadurch, daß das gegebene mathematische Problem durch ein vereinfachtes Problem ersetzt wird.
Ein Beispiel dafür ist die numerische Integration:
Das bestimmte Integral
Das 'numerische' Ergebnis lautet in diesem Fall ![]() , d.h. es tritt ein
(absoluter) Verfahrensfehler
, d.h. es tritt ein
(absoluter) Verfahrensfehler
Die Tatsache, daß für die Abspeicherung einer reellen Zahl (genauer gesagt: für deren Mantisse) nur eine endliche Anzahl von Bits zur Verfügung steht, ist die Ursache für die in fast 1.1 jedem Computerprogramm auftretenden, unvermeidlichen 1.2 Rundungsfehler.
Ein simples Beispiel:
Rechnung "von Hand": Computer (7 sign. Stellen):
123456.789 0.1234568E+06
+ 9.876543 + 0.9876543E+01
---------------- ----------------
123466.665543 0.1234667E+06
=8cm
Struktogramm 2Demonstration Rundungsfehler-Effektwert:=0.1
sum:=0.0i=1(1)50sum:=sum + wertprint: sum
Ein weiteres Beispiel: Die Auswertung des Struktogramms 2
zeigt ein auf den ersten Blick unverständliches
Phänomen:
Auf dem PC lautet das Ergebnis ![]() , d.h. man erhält einen
Rundungsfehlereffekt, obwohl nur 50mal die Konstante
, d.h. man erhält einen
Rundungsfehlereffekt, obwohl nur 50mal die Konstante ![]() aufaddiert wird,
die ja exakt abgespeichert werden kann.
aufaddiert wird,
die ja exakt abgespeichert werden kann.
Die Ursache für diesen Effekt ist darin begründet, daß die Zahl ![]() im Dezimalsystem zwar ohne Schwierigkeiten hingeschrieben werden kann, nicht
aber im vom Computer verwendeten Dualsystem. In diesem ist
im Dezimalsystem zwar ohne Schwierigkeiten hingeschrieben werden kann, nicht
aber im vom Computer verwendeten Dualsystem. In diesem ist ![]() nämlich
periodisch:
nämlich
periodisch:
Im folgenden soll das Fehlerverhalten von Computerprogrammen an Hand einiger typischer Beispiele demonstriert werden. Es sollen dabei Möglichkeiten gezeigt werden, wie man Verfälschungen von Resultaten auf Grund von Verfahrens- und Rundungsfehlern erkennen bzw. möglichst klein halten kann.
Das erste Beispiel zeigt, wie die Rundungsfehler bei der Auswertung eines mathematischen Ausdrucks durch geeignete Umformulierung des Algorithmus reduziert werden können.
Es geht um die numerische Auswertung des Ausdruckes
Programmiert man nun die Formel ohne weitere Umformung, also etwa
Tab.1.1: Numerische Auswertung von F(x) bzw. F1(x).
| x | F | F1 |
Bei den F-Werten in der obigen Tabelle fallen 2 Dinge auf:
Dieses Verhalten ist leicht erklärbar:
Soweit die Fehlerdiagnose. Die Therapie ist in diesem Fall sehr einfach:
Formt man nämlich ![]() in
in
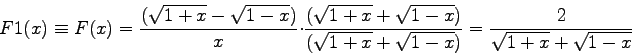
Ein weiteres Beispiel ([9], S.178) soll demonstrieren, daß man auch bei (scheinbar) eindeutigen Problemen in Schwierigkeiten geraten kann, wenn man bekannte Formeln 'einfach drauflos programmiert'.
Es geht um die numerische Auswertung quadratischer Gleichungen
Die wohlbekannten Lösungen lauten
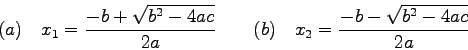
Eine Zusammenfassung dieser Ausdrücke führt zum folgenden Algorithmus:
Das Grundprinzip einer numerischen Differentiation besteht darin, daß man den gewünschten Differentialquotienten durch einen entsprechenden Differenzenquotienten ersetzt, also z.B.
Aus (1.3) geht hervor, daß der Differenzenquotient für die
Schrittweite ![]() zur ersten Ableitung der Funktion
zur ersten Ableitung der Funktion ![]() an der
Stelle
an der
Stelle ![]() konvergiert. Für eine endliche Schrittweite
konvergiert. Für eine endliche Schrittweite ![]() ist
natürlich mit einem Verfahrensfehler
ist
natürlich mit einem Verfahrensfehler ![]() zu rechnen,
wobei
zu rechnen,
wobei ![]() mit kleiner werdendem
mit kleiner werdendem ![]() abnehmen wird.
abnehmen wird.
Theoretische Überlegungen zeigen, daß ![]() die Form
die Form
Trägt man nun ![]() in Abhängigkeit von
in Abhängigkeit von ![]() in einem
doppelt-logarithmischen Diagramm auf, so ergibt sich als
Fehlerkurve die lineare Beziehung
in einem
doppelt-logarithmischen Diagramm auf, so ergibt sich als
Fehlerkurve die lineare Beziehung
Offensichtlich ist der Zusammenhang (1.4) für den Bereich
![]() sehr gut erfüllt. Für größere und für kleinere
Schrittweiten zeigt jedoch das 'wahre' Fehlerverhalten starke Abweichungen
vom theoretisch zu erwartenden Verfahrensfehler.
sehr gut erfüllt. Für größere und für kleinere
Schrittweiten zeigt jedoch das 'wahre' Fehlerverhalten starke Abweichungen
vom theoretisch zu erwartenden Verfahrensfehler.
Die Ursachen dafür sind die folgenden:
Die Abhängigkeit des Rundungsfehlers von ![]() entspricht keiner glatten
Kurve, hat aber tendenziell die Form
entspricht keiner glatten
Kurve, hat aber tendenziell die Form
Aus dem bisher Gesagten ergeben sich die folgenden wichtigen Konsequenzen:
Eine Reduktion dieses minimalen Fehlers kann auf zwei Arten geschehen:
Zusammenfassend kann gesagt werden:
Die Fehlerdiagnose in diesem Beispiel (und in vielen Bereichen der
numerischen Mathematik) wird dadurch entscheidend erleichtert, daß
unter bestimmten Voraussetzungen (hier: in einem bestimmten ![]() -Bereich)
der Verfahrensfehler den Rundungsfehler stark dominiert.
-Bereich)
der Verfahrensfehler den Rundungsfehler stark dominiert.
In vielen Anwendungen ist die numerische Auswertung der Funktion
Die Integraldarstellung bzw. die Darstellung in Form einer Taylorreihe lautet:
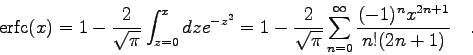
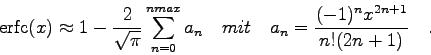
![\begin{displaymath}
a_{n} = \left[-\frac{x^{2}(2n-1)}{n(2n+1)}\right] a_{n-1}\qquad
\mbox{f\uml ur}\quad n=1,2,\ldots
\end{displaymath}](img132.gif)
=10cm
StruktogrammAuswertung einer Taylorreihex:= .....n:=0
sumnew:=x
a:=xn:=n+1
taylor:=sumnew
a:= -x*x*(2*n-1)/n/(2*n+1) * a
sumnew:=sumnew+asumnew=taylorprint: x, taylor
Aus dem vorher Gesagten geht hervor, daß alle Abweichungen der
numerischen von den
exakten Ergebnissen nur durch Rundungsfehler-Akkumulationen zustande kommen.
Dies kann man sofort erkennen, wenn man die Auswertung sowohl mit einfacher
als auch mit doppelter Genauigkeit durchführt. Die Ergebnisse dieses Tests
für eine Reihe von ![]() sind in der Tabelle 1.2, Spalte 2, angegeben.
sind in der Tabelle 1.2, Spalte 2, angegeben.
Aus dem Vergleich der Ergebnisse für die Auswertung der Taylorreihe ergibt
sich, daß die numerische Berechung von erfc![]() für kleine Argumente
für kleine Argumente
![]() sehr gut funktioniert, für größere
sehr gut funktioniert, für größere ![]() jedoch total versagt.
jedoch total versagt.
In diesem Argumentbereich muß ein anderer Algorithmus verwendet
werden.
Dafür bietet sich ein sogenannter Kettenbruch [11] an, der die Form
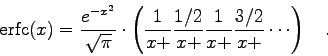
Im konkreten Fall wurde der Kettenbruch jeweils für 31 und für 61 Terme ausgewertet, wieder sowohl mit einfacher als auch mit doppelter Genauigkeit. Aus dem Vergleich der Ergebnisse (Tabelle 1.2, dritte und vierte Spalte) können die folgenden Schlüsse gezogen werden:
Tab.1.2: Auswertung der Funktion erfc![]() mittels der Taylorreihe bzw. des
Kettenbruches. Alle Ergebnisse sind in halb-exponentieller Schreibweise
mit 7 Mantissenstellen angegeben, wobei der Exponent E eine Berechnung in
einfacher Genauigkeit bedeutet, der Exponent D eine Berechnung in doppelter
Genauigkeit.
mittels der Taylorreihe bzw. des
Kettenbruches. Alle Ergebnisse sind in halb-exponentieller Schreibweise
mit 7 Mantissenstellen angegeben, wobei der Exponent E eine Berechnung in
einfacher Genauigkeit bedeutet, der Exponent D eine Berechnung in doppelter
Genauigkeit.
| x | Taylorreihe | Kettenbruch | Kettenbruch |
|
|
31 Terme | 61 Terme | |
| 0.01 | 0.9887166E+00 | 0.1261318E+02 | 0.9042203E+01 |
| 0.9887166D+00 | 0.1261318D+02 | 0.9042202D+01 | |
| 0.1 | 0.8875371E+00 | 0.1401417E+01 | 0.1131721E+01 |
| 0.8875371D+00 | 0.1401417D+01 | 0.1131721D+01 | |
| 0.5 | 0.4795001E+00 | 0.4802107E+00 | 0.4795305E+00 |
| 0.4795001D+00 | 0.4802107D+00 | 0.4795305D+00 | |
| 1. | 0.1572992E+00 | 0.1572995E+00 | 0.1572992E+00 |
| 0.1572992D+00 | 0.1572995D+00 | 0.1572992D+00 | |
| 2. | 0.4677685E-02 | 0.4677735E-02 | 0.4677735E-02 |
| 0.4677735D-02 | 0.4677735D-02 | 0.4677735D-02 | |
| 3. | 0.2991446E-04 | 0.2209050E-04 | 0.2209050E-04 |
| 0.2209050D-04 | 0.2209050D-04 | 0.2209050D-04 | |
| 4. | 0.2364931E-02 | 0.1541726E-07 | 0.1541726E-07 |
| 0.1544033D-07 | 0.1541726D-07 | 0.1541726D-07 | |
| 5. | 0.4645361E+02 | 0.1537460E-11 | 0.1537460E-11 |
| 0.5458862D-07 | 0.1537460D-11 | 0.1537460D-11 |
Als Zusammenfassung der Ergebnisse kann folgendes festgestellt werden:
Die Taylorreihen-Auswertung gibt bis ca. ![]() Ergebnisse mit mind. 7 sicheren
Ziffern.
Ergebnisse mit mind. 7 sicheren
Ziffern.
Die Kettenbruch-Auswertung mit 31 Termen gibt ab ca. ![]() Ergebnisse mit
mind. 7 sicheren Ziffern.
Ergebnisse mit
mind. 7 sicheren Ziffern.
Viele numerische Verfahren beruhen auf Rekursionsformeln vom Typus
Bei der Anwendung solcher Formeln muß besonders auf die Stabilität des Algorithmus geachtet werden:
Ein Algorithmus heißt stabil oder instabil, je nachdem ein im n-ten Rechenschritt zugelassener Rechnungsfehler bei exakter Rechnung in den Folgeschritten abnimmt oder anwächst (aus [2], S.9).
Ein sehr instruktives Beispiel stellt in diesem Zusammenhang die numerische Auswertung von sphärischen Besselfunktionen mittels einer ,,Vorwärts-Rekursion`` dar:
Tab.1.3: Numerische Berechnung der sphärischen Besselfunktionen der Ordnungen 0-9 mittels Vorwärts-Rekursion.
einfache Gen. doppelte Gen.
x = 0.3000
L= 0 0.9850674E+00 0 0.9850674D+00
1 0.9910274E-01 1 0.9910289D-01
2 0.5960023E-02 2 0.5961525D-02
3 0.2309625E-03 3 0.2558598D-03
4 -.5708978E-03 4 0.8536426D-05
5 -.1735790E-01 5 0.2329701D-06
6 -.6358853E+00 6 0.5811086D-08
7 -.2753767E+02 7 0.1884359D-07
8 -.1376248E+04 8 0.9363682D-06
9 -.7795982E+05 9 0.5304202D-04
x = 1.0000
L= 0 0.8414710E+00 0 0.8414710D+00
1 0.3011687E+00 1 0.3011687D+00
2 0.6203508E-01 2 0.6203505D-01
3 0.9006739E-02 3 0.9006581D-02
4 0.1012087E-02 4 0.1011016D-02
5 0.1020432E-03 5 0.9256116D-04
6 0.1103878E-03 6 0.7156936D-05
7 0.1332998E-02 7 0.4790142D-06
8 0.1988459E-01 8 0.2827691D-07
9 0.3367050E+00 9 0.1693277D-08
x = 10.0000
L= 0 -.5440211E-01 0 -.5440211D-01
1 0.7846694E-01 1 0.7846694D-01
2 0.7794219E-01 2 0.7794219D-01
3 -.3949584E-01 3 -.3949584D-01
4 -.1055893E+00 4 -.1055893D+00
5 -.5553451E-01 5 -.5553451D-01
6 0.4450132E-01 6 0.4450132D-01
7 0.1133862E+00 7 0.1133862D+00
8 0.1255780E+00 8 0.1255780D+00
9 0.1000964E+00 9 0.1000964D+00
x = 20.0000
L= 0 0.4564726E-01 0 0.4564726D-01
1 -.1812174E-01 1 -.1812174D-01
2 -.4836553E-01 2 -.4836552D-01
3 0.6030358E-02 3 0.6030359D-02
4 0.5047615E-01 4 0.5047615D-01
5 0.1668391E-01 5 0.1668391D-01
6 -.4130000E-01 6 -.4130000D-01
7 -.4352891E-01 7 -.4352891D-01
8 0.8653319E-02 8 0.8653319D-02
9 0.5088423E-01 9 0.5088423D-01
Die Ergebnisse von Tabelle 1.3 zeigen deutlich, daß - insbesondere für
kleine Argumente ![]() - das verwendete Verfahren stark instabil ist.
Diese Instabilität führt mit steigender Ordnung der Besselfunktion
zu einem völligen Versagen des Verfahrens.
- das verwendete Verfahren stark instabil ist.
Diese Instabilität führt mit steigender Ordnung der Besselfunktion
zu einem völligen Versagen des Verfahrens.
Für größere Argumente von ![]() wird die Stabilität des Verfahrens
zunehmend besser!
wird die Stabilität des Verfahrens
zunehmend besser!
Um auch im Bereich kleiner Argumente brauchbare numerische Ergebnisse zu erhalten, muß von der bisher verwendeten ,,Vorwärts-Rekursion`` auf eine ,,Rückwärts-Rekursion`` übergegangen werden:
Wegen der Willkür von ![]() sind die so erhaltenen Ergebnisse
mit einem Verfahrensfehler behaftet, der umso kleiner ist, je größer
der Startindex
sind die so erhaltenen Ergebnisse
mit einem Verfahrensfehler behaftet, der umso kleiner ist, je größer
der Startindex ![]() gewählt wurde.
Um eine Abschätzung von
gewählt wurde.
Um eine Abschätzung von ![]() zu erhalten, wurde die Auswertung
zweimal durchgeführt, und zwar mit
zu erhalten, wurde die Auswertung
zweimal durchgeführt, und zwar mit ![]() und mit
und mit ![]() . In beiden
Fällen wurde die Rechnung sowohl mit einfacher als auch mit doppelter
Genauigkeit durchgeführt.
. In beiden
Fällen wurde die Rechnung sowohl mit einfacher als auch mit doppelter
Genauigkeit durchgeführt.
Die Ergebnisse dieses Tests sind in der Tabelle 1.4 zusammengefaßt.
Es zeigt sich, daß die Rückwärts-Rekursion für den ganzen untersuchten
![]() -Bereich einen sehr stabilen Algorithmus darstellt: Die Ergebnisse von
einfacher und doppelter Genauigkeit unterscheiden sich erst in der
siebenten Ziffer der Mantissen um maximal zwei Einheiten.
Was den Verfahrensfehler betrifft, so ist mit steigendem Argument
-Bereich einen sehr stabilen Algorithmus darstellt: Die Ergebnisse von
einfacher und doppelter Genauigkeit unterscheiden sich erst in der
siebenten Ziffer der Mantissen um maximal zwei Einheiten.
Was den Verfahrensfehler betrifft, so ist mit steigendem Argument ![]() eine
steigende Tendenz dieses Fehlers zu beobachten.
eine
steigende Tendenz dieses Fehlers zu beobachten.
Resumee aus den Tabellen 1.3 und 1.4:
Tab.1.4: Numerische Berechnung der sphärischen Besselfunktionen der Ordnungen 0-9 mittels Rückwärts-Rekursion.
einfache Genauigkeit doppelte Genauigkeit
rueckwaerts(18) rueckwaerts(27) rueckwaerts(18) rueckwaerts(27)
x = 0.3000
L= 0 0.9850674E+00 0.9850674E+00 0.9850674D+00 0.9850674D+00
1 0.9910290E-01 0.9910290E-01 0.9910289D-01 0.9910289D-01
2 0.5961526E-02 0.5961525E-02 0.5961525D-02 0.5961525D-02
3 0.2558598E-03 0.2558598E-03 0.2558598D-03 0.2558598D-03
4 0.8536426E-05 0.8536425E-05 0.8536426D-05 0.8536426D-05
5 0.2329583E-06 0.2329583E-06 0.2329583D-06 0.2329583D-06
6 0.5378445E-08 0.5378444E-08 0.5378444D-08 0.5378444D-08
7 0.1076069E-09 0.1076069E-09 0.1076069D-09 0.1076069D-09
8 0.1899475E-11 0.1899474E-11 0.1899474D-11 0.1899474D-11
9 0.2999847E-13 0.2999847E-13 0.2999847D-13 0.2999847D-13
x = 1.0000
L= 0 0.8414710E+00 0.8414710E+00 0.8414710D+00 0.8414710D+00
1 0.3011687E+00 0.3011687E+00 0.3011687D+00 0.3011687D+00
2 0.6203505E-01 0.6203505E-01 0.6203505D-01 0.6203505D-01
3 0.9006580E-02 0.9006579E-02 0.9006581D-02 0.9006581D-02
4 0.1011016E-02 0.1011016E-02 0.1011016D-02 0.1011016D-02
5 0.9256115E-04 0.9256114E-04 0.9256116D-04 0.9256116D-04
6 0.7156936E-05 0.7156935E-05 0.7156936D-05 0.7156936D-05
7 0.4790134E-06 0.4790133E-06 0.4790134D-06 0.4790134D-06
8 0.2826499E-07 0.2826498E-07 0.2826499D-07 0.2826499D-07
9 0.1491376E-08 0.1491376E-08 0.1491377D-08 0.1491377D-08
x = 10.0000
L= 0 -.5440211E-01 -.5440211E-01 -.5440211D-01 -.5440211D-01
1 0.7846695E-01 0.7846695E-01 0.7846695D-01 0.7846694D-01
2 0.7794219E-01 0.7794220E-01 0.7794220D-01 0.7794219D-01
3 -.3949586E-01 -.3949586E-01 -.3949585D-01 -.3949584D-01
4 -.1055893E+00 -.1055893E+00 -.1055893D+00 -.1055893D+00
5 -.5553451E-01 -.5553451E-01 -.5553451D-01 -.5553451D-01
6 0.4450133E-01 0.4450133E-01 0.4450133D-01 0.4450132D-01
7 0.1133862E+00 0.1133862E+00 0.1133862D+00 0.1133862D+00
8 0.1255780E+00 0.1255780E+00 0.1255780D+00 0.1255780D+00
9 0.1000964E+00 0.1000964E+00 0.1000964D+00 0.1000964D+00
x = 20.0000
L= 0 0.4564727E-01 0.4564726E-01 0.4564726D-01 0.4564726D-01
1 -.8801447E-01 -.1812270E-01 -.8801444D-01 -.1812269D-01
2 -.5884944E-01 -.4836567E-01 -.5884943D-01 -.4836567D-01
3 0.7330211E-01 0.6031280E-02 0.7330208D-01 0.6031273D-02
4 0.8450518E-01 0.5047661E-01 0.8450516D-01 0.5047661D-01
5 -.3527479E-01 0.1668320E-01 -.3527476D-01 0.1668320D-01
6 -.1039063E+00 -.4130086E-01 -.1039063D+00 -.4130085D-01
7 -.3226432E-01 -.4352875E-01 -.3226432D-01 -.4352875D-01
8 0.7970807E-01 0.8654292E-02 0.7970804D-01 0.8654284D-02
9 0.1000162E+00 0.5088490E-01 0.1000161D+00 0.5088490D-01