Nächste Seite: Interpolation von Punktmengen. Aufwärts: Numerische Methoden in der Vorherige Seite: Einführung
Gegeben sind die ![]() Gleichungen
Gleichungen
wobei die ![]() und die
und die ![]() reellwertige Größen sind.
Außerdem soll gelten:
reellwertige Größen sind.
Außerdem soll gelten:
Unter diesen Voraussetzungen stellt (2.1) ein reellwertiges,
lineares, inhomogenes Gleichungssystem ![]() -ter Ordnung dar.
Die Größen
-ter Ordnung dar.
Die Größen
![]() , welche die gegebenen Gleichungen
simultan erfüllen, nennt man die Lösungen des Systems.
, welche die gegebenen Gleichungen
simultan erfüllen, nennt man die Lösungen des Systems.
(2.1) wird gewöhnlich in Form der Matrixgleichung
Vom theoretischen Standpunkt aus bereitet die Lösung von (2.1)
keinerlei Schwierigkeiten, solange die Determinante der
Koeffizientenmatrix ![]() nicht verschwindet, solange also das
Problem nicht singulär ist:
nicht verschwindet, solange also das
Problem nicht singulär ist:
In diesem Fall kann das Problem mit Hilfe der Cramer'schen Regel
angegangen werden. In der Praxis zeigt sich jedoch, daß die Anwendung
dieser Regel für ![]() recht kompliziert und aus verschiedenen
Gründen für die Anwendung am Computer ungeeignet ist.
recht kompliziert und aus verschiedenen
Gründen für die Anwendung am Computer ungeeignet ist.
Wie auch in anderen Bereichen der numerischen Mathematik gibt es auch hier zwei Gruppen von Methoden:
Diese enthalten keine Verfahrensfehler und führen deshalb - abgesehen von Rundungsfehler-Einflüssen - stets zur exakten Lösung. Allerdings können Rundungsfehler gerade bei direkten Verfahren, die häufig sehr rechenintensive Algorithmen aufweisen, massiv in Erscheinung treten.
Als Beispiel dazu wird im folgenden das Eliminationsverfahren von Gauss in der Formulierung von Doolittle und Crout (LU decomposition) behandelt.
zeichnen sich oft durch einen besonders einfachen Rundungsfehler-stabilen und Speicherplatz-sparenden Algorithmus aus, sie haben jedoch den Nachteil, daß sie nicht in jedem Fall konvergieren, also nicht auf alle an sich lösbaren linearen Gleichungssysteme angewendet werden können.
Außerdem erhält man auch im Falle der Konvergenz nie die exakte Problemlösung, sondern nur eine mit einem Abbruchfehler behaftete Näherungslösung.
Als Beispiel für ein Iterationsverfahren zur Lösung linearer Gleichungssysteme steht in diesem Kapitel das Gauss-Seidel-Verfahren.
Bei allen direkten Methoden geht es letzten Endes darum, das gegebene System
Die Gauss'sche Elimination besteht im wesentlichen aus zwei Schritten,
nämlich aus der Überführung von
![]() in das äquivalente
System
in das äquivalente
System
![]() und der Lösung dieses Systems mittels einer
Rück-Substitution.
und der Lösung dieses Systems mittels einer
Rück-Substitution.
Das Verfahren beruht auf einem Satz aus der linearen Algebra:
Ein lineares Gleichungssystem bleibt unverändert, wenn zu einer
seiner Gleichungen eine Linearkombination der restlichen Zeilen addiert wird.
Doolittle und Crout haben nun gezeigt, daß der Gauss'sche Algorithmus wie
folgt formuliert werden kann: Eine reelle Matrix ![]() kann stets als Produkt
zweier reeller Matrizen
kann stets als Produkt
zweier reeller Matrizen ![]() und
und ![]() dargestellt werden, also
dargestellt werden, also
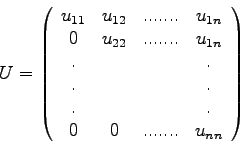
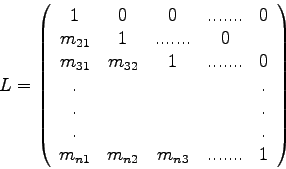
Man nennt die Zerlegung (2.4) einer Matrix ![]() die
die ![]() -
Zerlegung (
-
Zerlegung (![]() decomposition) von
decomposition) von ![]() .
.
Ohne Ableitung: ein einfacher Formelapparat für die LU-Zerlegung.
Die Umformung erfolgt spaltenweise, also
![]() :
:
Da die Hauptdiagonalelemente von ![]() stets Einser sind, braucht man diese
Werte (die
stets Einser sind, braucht man diese
Werte (die ![]() ) nicht extra abzuspeichern, sondern man kann alle
relevanten Werte in einer
) nicht extra abzuspeichern, sondern man kann alle
relevanten Werte in einer ![]() x
x ![]() -Matrix
(der 'LU-Matrix') unterbringen:
-Matrix
(der 'LU-Matrix') unterbringen:
Die Aufspaltung der Matrix ![]() in die Matrizen
in die Matrizen ![]() und
und ![]() kann nun zur
Berechnung des Lösungsvektors herangezogen werden:
kann nun zur
Berechnung des Lösungsvektors herangezogen werden:
Bei der konkreten Anwendung des Doolittle-Crout-Verfahrens geht man am besten so vor, daß man zwei Programme verwendet, von denen eines die LU-Zerlegung der Koeffizientenmatrix durchführt, während das zweite den Lösungsvektor unter Verwendung der Formeln (2.10-2.13) berechnet.
an Hand einer allgemeinen 3x3-Matrix.
Gegeben:

j = 1: erste Spalte
| (2.6) | i=1 |
|
| i=2 |
|
|
| i=3 |
|
|
| . | ||
| . | ||
| (2.7) |
|
|
| . | ||
| . | ||
| (2.8) | i=2 |
|
| i=3 |
|
Speichert man nun die eben berechneten Koeffizienten ![]() ,
, ![]() und
und
![]() anstelle der entsprechenden und nie wieder gebrauchten
Koeffizienten der Matrix A ab, so ergibt sich die Matrix
anstelle der entsprechenden und nie wieder gebrauchten
Koeffizienten der Matrix A ab, so ergibt sich die Matrix
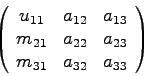
j=2: zweite Spalte
| (2.5) | i=1 | |
| . | ||
| . | ||
| (2.6) | i=2 |
|
| i=3 |
|
|
| . | ||
| . | ||
| (2.7) |
|
|
| . | ||
| . | ||
| (2.8) | i=3 |
|
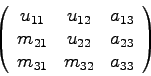
j=3: dritte Spalte
| (2.5) | i=1 | |
| i=2 |
|
|
| . | ||
| . | ||
| (2.6)i=3 |
|
|
| . | ||
| . | ||
| (2.7) |
|
![\begin{displaymath}\left(\begin{array}{ccc} u_{11} & u_{12} & u_{13} \\
m_{21}...
...{33} \end{array}\right)
= \mbox{LU-Matrix\quad [s. Glg.(2.9)]}\end{displaymath}](img210.gif)
Entscheidend ist also, daß durch die sukzessive Überspeicherung der
gegebenen Koeffizientenmatrix ![]() durch die Spalte für Spalte entstehende
LU-Matrix zu keiner Zeit ein Informationsmanko entsteht!
durch die Spalte für Spalte entstehende
LU-Matrix zu keiner Zeit ein Informationsmanko entsteht!
Da andererseits auch die neuen ![]() - bzw.
- bzw. ![]() -Werte stets
verschiedene Speicherplätze einnehmen, kann im Programm auf eine
unterschiedliche Bezeichnung der Elemente
-Werte stets
verschiedene Speicherplätze einnehmen, kann im Programm auf eine
unterschiedliche Bezeichnung der Elemente ![]() ,
, ![]() ,
, ![]() und
und ![]() überhaupt verzichtet werden, und alle diese Elemente werden
im Struktogramm 3 (LUDCMP) auf einem Feld A(,) abgespeichert!
überhaupt verzichtet werden, und alle diese Elemente werden
im Struktogramm 3 (LUDCMP) auf einem Feld A(,) abgespeichert!
Man spart damit sehr viel Speicherplatz, allerdings auf Kosten der
Lesbarkeit des Programms.
Angenommen, es existiert ein Programm, das die Auswertung eines inhomogenen Gleichungssystems nach der LU-Zerlegung durchführt. Die mittels dieses Programmes erhaltenen numerischen Ergebnisse enthalten keine Verfahrensfehler (direktes Verfahren!); jede Abweichung von den 'wahren' Ergebnissen muß daher auf Rundungsfehler zurückgehen.
Dazu ein konkretes Beispiel: Gegeben sei das folgende System von 3 Gleichungen:
Die numerische Auswertung (FORTAN, einfache Genauigkeit, d.h. 4 Byte pro reeller Zahl) liefert die folgende LU-Matrix und den folgenden Lösungsvektor:
| 0.1000000E+01 | 0.5923181E+07 | 0.1608000E+04 | |
| LU-Matrix: | 0.5923181E+07 | -.3508407E+14 | -.9524475E+10 |
| 0.6114000E+04 | 0.1032216E-02 | 0.9101371E+07 | |
| 0.9398398E+00 | |||
| x: | 0.1000000E+01 | ||
| 0.9995983E+00 |
Wie man sieht, ist der Rundungsfehler-Einfluß (besonders beim ![]() )
beträchtlich!
)
beträchtlich!
Wenn man nun die Reihenfolge der Gleichungen in (2.14)
abändert (was theoretisch natürlich keinen Einfluß auf den Lösungsvektor
hat), und zwar so, daß die ursprüngliche Reihenfolge ![]() übergeht
in die Reihenfolge
übergeht
in die Reihenfolge ![]() , so ergibt dasselbe Programm:
, so ergibt dasselbe Programm:
| 0.5923181E+07 | 0.3371160E+06 | -.7000000E+01 | |
| LU-Matrix: | 0.1032216E-02 | -.3459764E+03 | 0.9101372E+07 |
| 0.1688282E-06 | -.1712019E+05 | 0.1558172E+12 | |
| 0.9999961E+00 | |||
| x: | 0.1000068E+01 | ||
| 0.1000000E+01 |
| 0.5923181E+07 | 0.3371160E+06 | -.7000000E+01 | |
| LU-Matrix: | 0.1688282E-06 | 0.5923181E+07 | 0.1608000E+04 |
| 0.1032216E-02 | -.5841058E-04 | 0.9101372E+07 | |
| 0.1000000E+01 | |||
| x: | 0.1000000E+01 | ||
| 0.1000000E+01 |
Das bedeutet also, daß die richtige Zeilenfolge eines linearen Gleichungssystems einen entscheidenden Einfluß auf die Größe der Rundungsfehler und somit auf die Qualität der numerischen Lösung hat!
Was bedeutet nun 'richtige' Reihenfolge? Vergleicht man die ![]() -Werte
in den LU-Matrizen, so erkennt man sofort, daß die Rundungsfehler dann am
geringsten sind, wenn die Beträge der
-Werte
in den LU-Matrizen, so erkennt man sofort, daß die Rundungsfehler dann am
geringsten sind, wenn die Beträge der ![]() -Werte möglichst klein
sind.
-Werte möglichst klein
sind.
Um die ![]() so klein als möglich zu halten, müssen die in der Gleichung
(2.8) auftretenden
so klein als möglich zu halten, müssen die in der Gleichung
(2.8) auftretenden ![]() -Werte dem Betrage nach möglichst
groß sein. Dies kann einfach dadurch erreicht werden, daß man aus
allen
-Werte dem Betrage nach möglichst
groß sein. Dies kann einfach dadurch erreicht werden, daß man aus
allen ![]() nach Glg. (2.6) das betragsgrößte Element
bestimmt
und jene Zeile, in welcher dieses Element vorkommt, mit der
nach Glg. (2.6) das betragsgrößte Element
bestimmt
und jene Zeile, in welcher dieses Element vorkommt, mit der ![]() -ten Zeile
vertauscht. Erst danach werden die Gleichungen (2.7) und (2.8)
ausgewertet.
-ten Zeile
vertauscht. Erst danach werden die Gleichungen (2.7) und (2.8)
ausgewertet.
Eine derartige Strategie nennt man eine LU-Zerlegung mit teilweiser
Pivotisierung.
In der Regel hat man - vor allem bei Systemen höherer Ordnung - ohne
Pivotisierung keine Chance auf korrekte Ergebnisse. Es gibt aber auch
(s. [2], S. 56) Gleichungssysteme, bei welchen die LU-Decomposition
auch ohne Pivotisierung numerisch stabil ist, nämlich dann, wenn die
Koeffizientenmatrix symmetrisch, tridiagonal, zyklisch tridiagonal,
diagonal-dominant bzw. allgemein positiv definit ist.
Es ist klar, daß mit der Strategie der teilweisen Pivotisierung auch das
Nullwerden eines
Diagonalelementes ![]() und die damit auftretenden Probleme in
Glg.(2.8) vermieden werden können. Stellt sich nämlich heraus,
daß während der Rechnung alle
und die damit auftretenden Probleme in
Glg.(2.8) vermieden werden können. Stellt sich nämlich heraus,
daß während der Rechnung alle
![]() simultan
verschwinden, ist die Koeffizientenmatrix singulär und das
Gleichungssystem mit dem gegebenen Verfahren nicht lösbar!
simultan
verschwinden, ist die Koeffizientenmatrix singulär und das
Gleichungssystem mit dem gegebenen Verfahren nicht lösbar!
Die mit Hilfe direkter Methoden ermittelte Lösung eines linearen Gleichungssystems ist meist nicht die exakte Lösung, weil
Wenn kleine Änderungen in den Ausgangsdaten große Änderungen in der Lösung hervorrufen, spricht man von einem schlecht konditionierten System (s. Abb. 2.1).
Die sog. Konditionszahl der Koeffizientenmatrix kann dabei als Maß für die Güte der erhaltenen Näherungslösung für den Lösungsvektor verwendet werden.
In der mathematischen Literatur wird eine Reihe von Konditionszahlen
diskutiert. Im folgenden Programm LUDCMP ist die Berechnung der sog.
Hadamarschen Konditionszahl der Matrix ![]() inkludiert, welche
in der Form [2]
inkludiert, welche
in der Form [2]
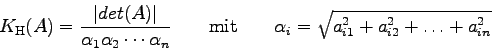
Quelle: [9], S.38f; [10], S. 46f (mit geringen Änderungen).
Das Programm LUDCMP (LU DeCoMPosition) führt eine LU-Aufspaltung einer reellen quadratischen Matrix durch.
INPUT Parameter:
OUTPUT Parameter:
=15cm
Struktogramm 3LUDCMP(A,N,INDX,D,KHAD)KHAD:=1.0I=1(1)NSUM:=0.0J=1(1)NSUM:=SUM + A(I,J)**2KHAD:=KHAD*SQRT(SUM)D:=1.0J=1(1)NI=1(1)J-1SUM:=A(I,J)K=1(1)I-1SUM:=SUM-A(I,K)*A(K,J)A(I,J):=SUMAAMAX:=0.0I=J(1)NSUM:=A(I,J)K=1(1)J-1SUM:=SUM-A(I,K)*A(K,J)A(I,J):=SUM DUM:=![]() SUM
SUM![]() DUM
DUM ![]() AAMAXIMAX:=I AAMAX:=DUM......J
AAMAXIMAX:=I AAMAX:=DUM......J ![]() IMAXK=1(1)NDUM:=A(IMAX,K)
IMAXK=1(1)NDUM:=A(IMAX,K)
A(IMAX,K):=A(J,K)
A(J,K):=DUMD:=-D......INDX(J):=IMAXA(J,J) = 0.0A(J,J):=TINY......
...DUM:=1.0/A(J,J)I=J+1(1)NA(I,J):=A(I,J)*DUMD:=D*A(J,J)KHAD:=![]() D
D ![]() /KHAD(return)
/KHAD(return)
Anmerkungen zum Programm LUDCMP:
Quelle: [9], S. 39; [10], S. 47 (mit Änderungen).
Das Programm LUBKSB (LU BacKSuBstitution) berechnet den Lösungsvektor x
des Systems
![]() unter Verwendung der Gleichungen (2.10
- 2.13).
unter Verwendung der Gleichungen (2.10
- 2.13).
INPUT-Parameter:
OUTPUT Parameter:
Interner Vektor:
Struktogramm 4LUBKSB(A,N,INDX,B,X)I=1(1)NBB(I):=B(I)I=1(1)NLL:=INDX(I)
SUM:=BB(LL)
BB(LL):=BB(I)J=1(1)I-1SUM:=SUM-A(I,J)*Y(J)Y(I):=SUMI=N(-1)1SUM:=Y(I)J=I+1(1)NSUM:=SUM-A(I,J)*X(J)X(I):=SUM/A(I,I)(return)
||---------------------------||
|| LUDCMP(A,N,INDX,D,KHAD) ||
||---------------------------||
|| LUBKSB(A,N,INDX,B,X) ||
||---------------------------||
Ein wesentlicher Vorteil des hier vorgestellten Verfahrens besteht darin,
daß bei Auftreten verschiedener inhomogener Vektoren ![]() ,
,
![]() , ..., aber gleichbleibender Koeffizientenmatrix
, ..., aber gleichbleibender Koeffizientenmatrix ![]() die
LU-Zerlegung nur einmal durchgeführt werden muß:
die
LU-Zerlegung nur einmal durchgeführt werden muß:
||-------------------------||
|| LUDCMP(A,N,INDX,D,KHAD) ||
||-------------------------||
|
||-------------------------||
|| LUBKSB(A,N,INDX,B1,X1) ||
|| LUBKSB(A,N,INDX,B2,X2) ||
|| . ||
|| . ||
||-------------------------||
Mit Hilfe der Programme LUDCMP und LUBKSB kann eine gegebene Matrix ![]() Spalte für Spalte invertiert werden:
Spalte für Spalte invertiert werden:
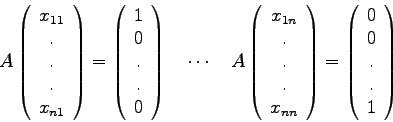
StruktogrammInvertierung einer MatrixA,N,INDX,D,KHADLUDCMPJ=1(1)NI=1(1)NVEKTOR(I):=0.0VEKTOR(J):=1.0A,N,INDX,VEKTOR,XLUBKSBI=1(1)NAINV(I,J):=X(I)
Für die Determinante der Matrix A gilt
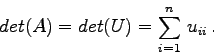
Gegeben ist die Matrix mit vier Zeilen und Spalten

Die Konditionszahl lautet ![]() = 0.752, das System
ist also gut konditioniert!
= 0.752, das System
ist also gut konditioniert!
Das numerische Ergebnis ist bis auf Maschinengenauigkeit exakt:
Das numerische Ergebnis ist fast bis auf Maschinengenauigkeit exakt (bis auf maximal zwei Einheiten in der siebenten Stelle hinterm Komma) und lautet:
Invertierte Matrix: .9379443E+00 -.6843720E-01 -.7960770E-01 -.8592076E-01 -.8852433E-01 .9059826E+00 -.9919081E-01 -.1055899E+00 -.1113511E+00 -.1169667E+00 .8784252E+00 -.1270733E+00 -.1354557E+00 -.1401826E+00 -.1438075E+00 .8516058E+00 Test-Matrix: .9999999E+00 .1126516E-07 .2518815E-08 -.1120211E-08 -.4888310E-08 .1000000E+01 -.6621389E-08 -.3829147E-08 -.2647183E-08 .5092004E-08 .9999999E+00 .1665558E-07 .7356128E-08 -.1727934E-07 -.1442864E-07 .1000000E+01
Die Test-Matrix stellt einfach das Multiplikations-Ergebnis: gegebene Matrix mal (numerisch) invertierte Matrix dar. Zu erwarten wäre im Idealfall die Einheitsmatrix.
Das numerische Ergebnis (auf Maschinengenauigkeit exakt) lautet
Es ist klar, daß die Genauigkeit der numerischen Lösung eines linearen Gleichungssystems durch die Maschinengenauigkeit begrenzt ist. Leider ist es in vielen Fällen so, daß diese Genauigkeit wegen auftretender Rundungsfehler-Kumulationen nicht erreicht wird.
In solchen Fällen gibt es die Möglichkeit einer iterativen Verbesserung der numerischen Lösung, deren (sehr einfache) Theorie nun kurz erläutert wird:
Die numerische Lösung des Systems
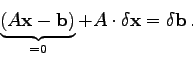
Das Struktogramm 5 zeigt die Lösung eines linearen
Gleichungssystems
mit anschließender iterativer Verbesserung des Lösungsvektors:
Dazu noch einige Anmerkungen:
Struktogramm 5Iterative Verbesserung des LösungsvektorsI=1(1)NJ=1(1)NASP(I,J):=A(I,J)A,N,INDX,D,KHADLUDCMPA,N,INDX,B,XLUBKSBI=1(1)NSUMDP:=-B(I)J=1(1)NSUMDP:=SUMDP + DBLE(ASP(I,J))*DBLE(X(J))RES(I):=SUMDPA,N,INDX,RES,DELXLUBKSBI=1(1)NX(I):=X(I)-DELX(I)(Bedingung, unter welcher die Iteration
verlassen wird)(Ausgabe und return)
Die Methode der partiellen Pivotisierung bewirkt eine entscheidende Reduktion der beim Gauss'schen Verfahren auftretenden Rundungsfehler. Dennoch kann bei schlecht konditionierten Gleichungssystemen der numerisch ermittelte Lösungsvektor deutlich fehlerbehaftet sein, wie das folgende Beispiel zeigt:
0.10000E+01 0.50000E+00 0.33333E+00 0.25000E+00 0.20000E+00 0.228333E+01 0.50000E+00 0.33333E+00 0.25000E+00 0.20000E+00 0.16667E+00 0.145000E+01 0.33333E+00 0.25000E+00 0.20000E+00 0.16667E+00 0.14286E+00 0.109286E+01 0.25000E+00 0.20000E+00 0.16667E+00 0.14286E+00 0.12500E+00 0.884530E+00 0.20000E+00 0.16667E+00 0.14286E+00 0.12500E+00 0.11111E+00 0.745640E+00
Die Koeffizientenmatrix stellt eine Hilbert-Matrix 5. Ordnung mit
den auf 5 signifikante Stellen gerundeten Komponenten
Das exakte Ergebnis wird im folgenden dem numerischen Ergebnis
![]() gegenübergestellt (FORTRAN, single precision). Weiters ist
zur Kontrolle der Vektor
gegenübergestellt (FORTRAN, single precision). Weiters ist
zur Kontrolle der Vektor
![]() ausgegeben:
ausgegeben:
|
|
|
|
| 1. | 0.9999459E+00 | 0.2283330E+01 |
| 1. | 0.1000955E+01 | 0.1450000E+01 |
| 1. | 0.9960009E+00 | 0.1092860E+01 |
| 1. | 0.1005933E+01 | 0.8845300E+00 |
| 1. | 0.9971328E+00 | 0.7456400E+00 |
Das Dilemma ist deutlich zu sehen: Obwohl einige Komponenten des numerisch erhaltenen Lösungsvektors beträchtlich vom exakten Wert abweichen, ist das lineare Gleichungssystem mit Maschinengenauigkeit erfüllt! Auch eine Nachiteration bringt keine Verbesserung der Ergebnisse.
Dieses Beispiel enthüllt noch ein weiteres ernstes Problem bei der Verwendung numerischer Methoden zur Lösung linearer Systeme: Es gibt trotz zahlreicher theoretischer Untersuchungen (s. z.B. [12], S.109ff) keine einfache, also in der Praxis einsetzbare Abschätzung des im Lösungsvektor enthaltenen Rundungsfehlers.
Eine weitere unangenehme Rundungsfehler-Konsequenz besteht darin, daß es bei der numerischen Auswertung praktisch unmöglich ist, klar zwischen singulären und fast-singulären Koeffizientenmatrizen zu unterscheiden. Im Programm wird eine Matrix dann als singulär erkannt, wenn alle Elemente einer Pivot-Spalte exakt Null sind. Da aber diese Elemente ihrerseits Ergebnisse arithmetischer Operationen sind, ist wegen der dabei auftretenden Rundungsfehler auch im Falle der Singularität der Koeffizientenmatrix nicht mit exakten Nullen zu rechnen (das folgende aus [12], S.63):
Die Lage wird dadurch besonders kompliziert, daß die scharfe mathematische Unterscheidung von singulären und nicht-singulären Matrizen nur in der Idealwelt des Mathematikers existiert. Sobald wir mit Matrizen in gerundeter Arithmetik arbeiten, wird die Unterscheidung notwendigerweise ungerechtfertigt. So können gewisse nicht-singuläre Matrizen als Ergebnis von durch die Rundungsfehler eingeführten Störungen singulär werden. Noch wahrscheinlicher wird eine wirklich singuläre vorgegebene Matrix durch den Rundungsfehler in eine benachbarte nicht-singuläre Matrix abgeändert.
Aus diesem Grund verzichten viele Programme auf eine
Singularitäts-Diagnose und überlassen diese dem Benutzer.
Im Programm LUDCMP wird zwar
abgefragt, ob im Laufe der Rechnung irgendein Diagonalelement ![]() exakt(!) Null ist, aber nur, um in diesem (unwahrscheinlichen) Fall eine
Division durch Null zu verhindern!
exakt(!) Null ist, aber nur, um in diesem (unwahrscheinlichen) Fall eine
Division durch Null zu verhindern!
Nachdem direkte Verfahren zur Lösung linearer Gleichungssysteme relativ rechen- und speicherplatz-intensiv sind, ist es in der Praxis von sehr großer Bedeutung, spezielle Koeffizientenmatrizen auszunutzen, um vereinfachte Algorithmen zu formulieren.
Eine Reihe wichtiger numerischer Verfahren (z.B. die Spline-Interpolation) führen zu linearen Gleichungssystemen der Form
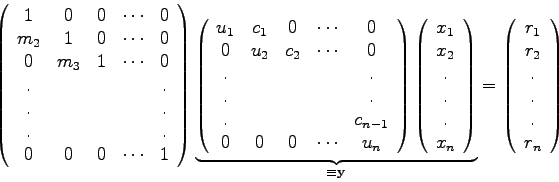
Quelle: [9], S. 43 (mit Änderungen).
Das Programm TRID berechnet den Lösungsvektor eines linearen, inhomogenen Gleichungssystems mit tridiagonaler Koeffizientenmatrix.
INPUT-Parameter:
OUTPUT-Parameter:
Interne Vektoren:
Struktogramm 6TRID(A,B,C,R,N,X)Y(1):=R(1)
U(1):=B(1)U(1) = 0.0(Abbruch mit Fehlermitteilung!)......J=2(1)NM:=A(J)/U(J-1)
U(J):=B(J)-M*C(J-1)U(J) = 0.0(Abbruch mit Fehlermitteilung!)......Y(J):=R(J)-M*Y(J-1)X(N):=Y(N)/U(N)J=N-1(-1)1X(J):=(Y(J)-C(J)*X(J+1))/U(J)(return)
Anmerkungen zu TRID:
Es kann jedoch gezeigt werden, daß bei allen sogenannten diagonal-
dominanten tridiagonalen Matrizen, d.h. bei solchen, die die Eigenschaft
![]() für alle
für alle
![]() haben, keine derartigen Probleme auftreten. Diese Feststellung
ist von Bedeutung, weil viele in der Praxis auftretenden tridiagonalen
Matrizen diese Eigenschaft der Diagonal-Dominanz haben!
haben, keine derartigen Probleme auftreten. Diese Feststellung
ist von Bedeutung, weil viele in der Praxis auftretenden tridiagonalen
Matrizen diese Eigenschaft der Diagonal-Dominanz haben!
In der Literatur findet man noch eine große Anzahl von Algorithmen bzw. Programmen für die numerische Behandlung von linearen Gleichungssystemen, deren Koeffizientenmatrizen besondere Strukturen haben. Insbesondere soll auf [2] und auf [9] hingewiesen werden, wo man Informationen zu den Themen: symmetrische Matrizen (Cholesky-Verfahren), zyklisch-tridiagonale Matrizen, fünfdiagonale Matrizen, allgemeine Bandmatrizen, Blockmatrizen usw. erhält.
Das Gauss-Seidel-Verfahren (sowie seine Variationen, die in der Literatur unter den Namen Einzelschrittverfahren, Gesamtschrittverfahren, Relaxationsverfahren, SOR-Verfahren usw. zu finden sind) ist ein iteratives Verfahren zur Lösung von linearen inhomogenen Gleichungssystemen.
Wie schon zu Beginn dieses Kapitels erwähnt wurde, weisen iterative Verfahren gegenüber den direkten Verfahren einige Vorteile (Einfachheit des Algorithmus usw.), aber auch Nachteile (eventuell Konvergenzprobleme) auf.
Der wichtigste Vorteil der iterativen Verfahren liegt aber wohl in der Tatsache, daß die gegebene Koeffizientenmatrix während des Iterationsprozesses nicht verändert wird. Dieser Vorteil wirkt sich - wie im folgenden gezeigt wird - ganz besonders positiv aus, wenn man lineare Gleichungssysteme von hoher Ordnung auszuwerten hat, die schwach besetzte Koeffizientenmatrizen haben.
Eine Matrix heißt schwach besetzt, wenn nur wenige ihrer Koeffizienten von Null verschieden sind.
Da sich einige sehr wichtige Probleme der Numerischen Mathematik (z.B. die Lösung von Randwertproblemen mittels der Differenzenmethode) auf lineare Gleichungssysteme mit schwach besetzten Matrizen zurückführen lassen, soll im folgenden vor allem auf derartige Probleme eingegangen werden.
Ausgangspunkt ist wieder das lineare System (2.1):
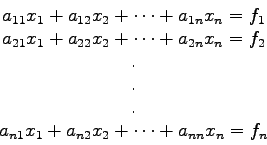
![\begin{displaymath}
x_{i}=x_{i}-\left( x_{i}+\frac{1}{a_{ii}} \left[\sum_{j=1(j\ne i)}^{n}
a_{ij} x_{j}-f_{i} \right] \right)
\end{displaymath}](img290.gif)
Auf diese Weise kann im Falle einer Konvergenz eine Folge von
Näherungsvektoren
Typisch für alle Iterationsverfahren sind die sogenannten Abbruchbedingungen, die festlegen, wann eine Iteration zu beenden ist.
In jedem Iterationsprogramm sollten zumindest die beiden folgenden Abbruchbedingungen enthalten sein:
Eine Bandmatrix ist eine Matrix, die nur entlang einiger Diagonalen Komponenten enthält, die von Null verschieden sind (s. Abbildung 2.2 (oben)).
Es ist sofort einzusehen, daß es vom Standpunkt der Speicherplatz-Ökonomie
ein Nonsens ist, eine solche Matrix als (![]() x
x ![]() )-Matrix
abzuspeichern. Die gesamte Information kann nämlich viel platzsparender
abgespeichert werden, wenn man die Diagonalen als Vektoren speichert
und über die Lage der einzelnen Diagonalen innerhalb der Matrix buchführt.
)-Matrix
abzuspeichern. Die gesamte Information kann nämlich viel platzsparender
abgespeichert werden, wenn man die Diagonalen als Vektoren speichert
und über die Lage der einzelnen Diagonalen innerhalb der Matrix buchführt.
Wie dies z.B. geschehen kann, ist in der Abbildung 2.2 (unten)
schematisch dargestellt:
![]() sei die Anzahl der in der Matrix vorkommenden Diagonalen. Die Lage jeder
Diagonale wird nun durch eine ganze Zahl angegeben, die angibt, wo sich diese
Diagonale relativ zur Hauptdiagonale befindet. Damit kann die
Abspeicherung der gesamten Information in einem zweidimensionalen Feld
sei die Anzahl der in der Matrix vorkommenden Diagonalen. Die Lage jeder
Diagonale wird nun durch eine ganze Zahl angegeben, die angibt, wo sich diese
Diagonale relativ zur Hauptdiagonale befindet. Damit kann die
Abspeicherung der gesamten Information in einem zweidimensionalen Feld
![]() erfolgen, wobei der Index
erfolgen, wobei der Index ![]() die jeweilige Matrixzeile bedeutet.
Der zweite Index (
die jeweilige Matrixzeile bedeutet.
Der zweite Index (![]() ) gibt an, um welche der
) gibt an, um welche der ![]() Diagonalen es sich handelt.
Zusätzlich wird ein INTEGER-Feld
Diagonalen es sich handelt.
Zusätzlich wird ein INTEGER-Feld ![]() mit den relativen Positionen
definiert:
mit den relativen Positionen
definiert:

Die Zuordnung der Matrixelemente ![]() (
(![]() -te Zeile,
-te Zeile,
![]() -te Spalte) zu den Elementen
-te Spalte) zu den Elementen ![]() ist somit gegeben durch
ist somit gegeben durch
Auf Grund all dieser Überlegungen ist es kein Problem, die Iterationsvorschrift (2.21) im Hinblick auf (2.22) zu variieren:
Anmerkung: In der Summe in Glg.(2.24)werden nur jene
Summanden zugelassen, für welche gilt:
Es erhebt sich nun die wichtige Frage, ob man es einem gegebenen linearen Gleichungssystem schon a priori 'ansieht', daß es Schwierigkeiten bei der Konvergenz geben wird.
Nun gibt es in der Literatur in der Tat eine ganze Reihe von Konvergenz- Kriterien, d.h. von Bedingungen, die im Falle ihrer Erfüllung die Konvergenz der Gauss-Seidel-Iteration sicherstellen. Solche Kriterien sind zwar hinreichend, aber i.a. nicht notwendig, d.h. auch manche Systeme, die diese Kriterien nicht erfüllen, können mittels des Gauss-Seidel- Verfahrens gelöst werden.
Aus diesem Grund möchte ich hier auf die Angabe von mathematisch formulierten Konvergenz-Kriterien verzichten und mich auf eine in der Praxis bewährte Faustregel beschränken:
Alle linearen Gleichungssysteme, in deren Koeffizientenmatrizen die Hauptdiagonalelemente die anderen Matrixelemente dominieren, haben gute Chancen auf eine Gauss-Seidel-Konvergenz.
Ein konvergentes Verhalten der Iteration bedeutet natürlich, daß der
auftretende Verfahrensfehler ![]() mit fortschreitender Iteration
immer kleiner wird, daß also gilt:
mit fortschreitender Iteration
immer kleiner wird, daß also gilt:
In der Praxis wird solange iteriert, bis der Korrekturvektor
![]() [Glg. (2.24)] genügend klein geworden ist.
Man verwendet in diesem Fall
als Abbruchkriterien die absolute Fehlerabfrage
[Glg. (2.24)] genügend klein geworden ist.
Man verwendet in diesem Fall
als Abbruchkriterien die absolute Fehlerabfrage
Achten Sie darauf, die Größe GEN nicht zu klein anzusetzen, da im Falle von schlecht konditionierten Problemen die entsprechende Rechengenauigkeit durch auftretende Rundungsfehler nicht erreicht werden kann!
Nun gibt
es jedoch die Aussage, daß iterative Methoden i.a. wesentlich geringere
Rundungsfehler aufweisen als die direkten Methoden. Es ist insbesondere
eine Eigenschaft von Iterationsmethoden, daß jeweils nur die Rundungsfehler
des letzten Iterationsschrittes einen Effekt haben: es gibt also
keine ![]() -Kumulation über alle Iterationen hinweg!
Auf Grund dieser Tatsache ist die Verwendung des Gauss-Seidel-Verfahrens
in manchen Fällen auch dann einem direkten Verfahren vorzuziehen, wenn es
höhere Rechenzeiten erfordert.
-Kumulation über alle Iterationen hinweg!
Auf Grund dieser Tatsache ist die Verwendung des Gauss-Seidel-Verfahrens
in manchen Fällen auch dann einem direkten Verfahren vorzuziehen, wenn es
höhere Rechenzeiten erfordert.
Das Programm GAUSEI (GAUss-SEIdel) berechnet den Lösungsvektor eines inhomogenen linearen Gleichungssystems mit einer allgemeinen Bandmatrix als Koeffizientenmatrix.
INPUT-Parameter:
OUTPUT-Parameter:
FEHLER hat nach der Exekution von GAUSEI den Wert 'falsch', wenn die geforderte Genauigkeit erreicht wurde, und den Wert 'wahr', wenn
wichtige interne Variable:
Programmstruktur von GAUSEI:
=15cm
Struktogramm 8GAUSEI(N,NDIAG,S,DIAG,F,TMAX,W,IREL,GEN,
LOES,T,FEHLER)FEHLER:= .false.
K0:=0K=1(1)NDIAGS(K) = 0K0:=K......K0 = 0FEHLER:= .true.
(return 'Keine Hauptdiagonale')......I=1(1)NLOES(I):=0.0DIAG(I,K0) = 0.0FEHLER:= .true.
(return 'Hauptdiagonale enthaelt Null')......T:=0ISCH:=0I=1(1)NS1:=0.0K=1(1)NDIAGJ:=S(K)+IK ![]() K0 .and. J
K0 .and. J ![]() 0 .and. J
0 .and. J ![]() NS1:=S1+DIAG(I,K)*LOES(J)......DX:=W*((S1-F(I))/DIAG(I,K0)+LOES(I)LOES(I):=LOES(I)-DXIREL = 1ERR:=
NS1:=S1+DIAG(I,K)*LOES(J)......DX:=W*((S1-F(I))/DIAG(I,K0)+LOES(I)LOES(I):=LOES(I)-DXIREL = 1ERR:=![]() DX/LOES(I)
DX/LOES(I) ![]() ERR:=
ERR:= ![]() DX
DX ![]() ERROR
ERROR ![]() GENISCH:=1......T:=T+1T
GENISCH:=1......T:=T+1T ![]() TMAX .or. ISCH=0ISCH=0print: 'Keine Konvergenz'
TMAX .or. ISCH=0ISCH=0print: 'Keine Konvergenz'
FEHLER:= .true.......(return)
Die Iterationsvorschrift (2.23)
Durch die richtige Wahl des Relaxationsparameters ![]() kann in manchen
Fällen die Konvergenzgeschwindigkeit außerordentlich erhöht werden.
Ein gutes Beispiel für diesen Effekt findet man in [7], S.192ff.
Iteriert man das einfache lineare System
kann in manchen
Fällen die Konvergenzgeschwindigkeit außerordentlich erhöht werden.
Ein gutes Beispiel für diesen Effekt findet man in [7], S.192ff.
Iteriert man das einfache lineare System
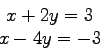
|
|
|
|
|
|
| |
|
| |
|
|
|
|
| |
|
| |
|
| |
|
|
|
|
| |
|
Es wäre eine enorme Effizienzsteigerung der Gauss-Seidel-Methode,
wenn man den idealen Relaxationsparameter
![]() a priori bestimmen könnte. Zu diesem Thema folgen nun einige
Anmerkungen:
a priori bestimmen könnte. Zu diesem Thema folgen nun einige
Anmerkungen:
Man kann zeigen, daß der Ausdruck
Wie gut diese Strategie funktioniert, wird in den Übungen zu dieser Vorlesung demonstriert.
In den vorigen Abschnitten wurde als Vorteil der Gauss-Seidel-Methode angegeben, daß die Koeffizientenmatrix sich während der Iteration nicht ändert, was vor allem im Falle schwach besetzter Bandmatrizen günstig ist, weil man nur die besetzten Diagonalen abspeichern muß.
Dies soll an Hand eines konkreten Beispiels dokumentiert werden, und zwar für die numerische Auswertung einer sehr bedeutenden partiellen Differentialgleichung, nämlich der Laplace-Gleichung. Unter Verwendung der Differenzenmethode wird diese Differentialgleichung samt ihren Nebenbedingungen in ein System von linearen Gleichungen umgewandelt. Die Ordnung dieses Systems ergibt sich dabei aus der Zahl der Stützpunkte im Grundgebiet der zu lösenden Laplace-Gleichung. Die folgende Abbildung 2.3 (a) zeigt, wie viele Prozent der Elemente der Koeffizientenmatrix als Funktion der Stützpunktzahl tatsächlich besetzt sind. Man sieht, daß dieser Wert ab etwa 200 Stützpunkten deutlich unter 10 Prozent liegt.
Wie sich das auf die im Arbeitsspeicher des Computers nötigen Speicherplätze auswirkt, ist in Abb. 2.3 (b) dargestellt.
 |
Überhuber ([22], S. 392) gibt ein Beispiel aus der
industriellen Anwendung linearer Methoden (Karosserie-Festigkeitsberechnung
im Automobilbau): Eine Matrix BCSSTK32 hat die Ordnung 44609, also
![]() Elemente; von diesen sind aber 'nur' 1029655
Nicht-Nullelemente, d. h. der Besetzungsgrad beträgt 0.05 %.
Elemente; von diesen sind aber 'nur' 1029655
Nicht-Nullelemente, d. h. der Besetzungsgrad beträgt 0.05 %.
.
Am Ende jedes Hauptkapitels dieses Skriptums finden Sie unter dem Titel 'Software-Angebot' Hinweise auf Programme, die Sie sich entweder kostenlos übers Internet beschaffen können (public domain (p.d.) Programme), oder die kommerziell vertrieben werden.
Quellen: (1) Bücher von Ch. Überhuber [21],
[22].
(2) Erfahrungen des Autors dieses Skriptums.
Diese Anmerkungen können auf Grund des riesigen Software-Angebotes nur erste Anregungen für Sie sein, dieses Angebot zu nutzen.
Zitat aus [21], S. 322:
Von herausragender Bedeutung für die rasche, einfache und effiziente
Beschaffung von frei erhältlicher (public domain)-Software aus dem
Numerik-Bereich ist der Internet-Dienst NETLIB (Dongara, Grosse,
'Distribution of Mathematical Software via Electronic Mail',
Comm. ACM 30 (1987), 403).
Auf Programme aus dem NETLIB kann über verschiedene Internet-Dienste
zugegriffen werden (email, FTP, Internet); am einfachsten ist ein
'Downladen' aus dem www-System. Ich werde mich im folgenden auf diese
Möglichkeit beschränken.
Zuvor noch ein weiteres Zitat ([22], S. 183) mit speziellem
Bezug auf das Kap. 2 dieses Skriptums:
Für die numerische Lösung linearer Gleichungssysteme gibt es,
mehr als in jedem anderen Gebiet der Numerischen Datenverarbeitung,
eine Fülle qualitativ hochwertiger Softwareprodukte: LAPACK, TEMPLATES,
ITPACK, NSPCG, SLAP, UMFPACK, Teile der IMSL- und NAG-Bibliotheken.
Die eigene Entwicklung von Software zur Lösung linearer Gleichungssysteme
wäre aus diesem Grund ein sehr unökonomisches Unterfangen.
Die wichtigsten Libraries für den Problemkreis "Lineare Gleichungssystemeßind die folgenden:
Umfangreiche Sammlung von F77-Programmen zu den
Themen
'Lösung linearer Gleichungssysteme', 'Eigenwertprobleme' u.a.
Die komplette aktuelle Bibliothek (31.5.2000) inklusive aller sog.
BLAS-Hilfsprogramme2.2umfaßt ca. 5 MByte und kann durch Anklicken von
lapack.tgz
downgeladen werden. Danach einfach auf Ihrem LINUX-Rechner dekomprimieren
und in die einzelnen Programme aufteilen:
gunzip -c lapack.tgz | tar xvf -Achtung: Alle Programme (ohne OBJ- und EXE-Files) in den 4 Datentypen REAL, DOUBLE PRECISION, COMPLEX und COMPLEX*16 benötigen ca. 34 MByte.
file dgesv.f dgesv.f plus dependencies prec double for Solves a general system of linear equations AX=B.Sie könnten nun durch Anklicken von dgesv.f das Programm speichern. Allerdings hat das i.a. wenig Sinn, da die meisten LAPACK-Programme eine ganze Kaskade von weiteren Programmen aufrufen. Es ist daher besser, diese ganze 'Programmfamilie' durch Anklicken von dgesv.f plus dependencies zu laden. Im erscheinenden Dialogfenster wählen Sie als "Packaging format" Tar-gzip, und die nötigen BLAS-Files laden Sie am besten gleich dazu.
gunzip -c netlibfiles.tgz | tar xvf -Damit haben Sie sofort, auf drei neu erstellte Verzeichnisse aufgeteilt, die gesamte Programmfamilie von dgesv.f zur Verfügung:
blas/blas2test.f blas/dgemm.f blas/dger.f blas/dscal.f blas/dswap.f blas/dtrsm.f blas/idamax.f blas/xerbla.f lapack/double/dgesv.f lapack/double/dgetf2.f lapack/double/dgetrf.f lapack/double/dgetrs.f lapack/double/dlaswp.f lapack/util/ieeeck.f lapack/util/ilaenv.f
Die folgende knappe Zusammenstellung gibt Ihnen eine Übersicht über das
LAPACK-Angebot ([22], S. 266). Die Begriffe simple drivers
und expert drivers bedeuten:
simple drivers: black box-Programme, die primär die
numerische Lösung der jeweiligen Problemstellung liefern.
expert drivers liefern neben den Lösungen auch noch zusätzliche
Informationen (Konditionsabschätzungen, Fehlerschranken usw.).

LAPACK bietet nur direkte Verfahren in FORTRAN-77. Diese Programmiersprache ist zwar immer noch weitverbreitet im technisch-naturwissenschaftlichen Bereich; da aber neue Fortranversionen wie F90, F95 sowie andere Sprachen wie C und C++ immer wichtiger werden, gibt es inzwischen auch schon die entsprechenden LAPACK-Routinen:
stellt ein Interface zu F77 dar, d. h. Sie benötigen auch die
LAPACK-F77 Programme. LAPACK95 erhalten Sie über
www.netlib.org/lapack95/index.html.
Downladen von lapack95.tgz und nachfolgende Dekomprimierung
erzeugt in Ihrer Directory das Unterverzeichnis LAPACK95. In diesem
gibt es das Verzeichnis SRC mit allen zur Verfügung stehenden
Routinen.
erhalten Sie über www.netlib.org/clapack.
Es handelt sich dabei um eine vollständige C-Implementierung
von LAPACK, wobei die Konvertierung von F77 in C automatisch erfolgte.
Der Nachteil dieses Vorgehens ist allerdings, daß CLAPACK
wertvolle Eigenschaften von C, wie z. B. dynamische Speicherallokation,
nicht nutzt.
Darüber hinaus können Sie nicht einfach irgendein einzelnes
CLAPACK-Programm
herunterladen, sondern es ist eine komplette Installation von
clapack.tgz (Version 3.0, ca. 6 MByte) erforderlich.
Dieser File enthält auch die Installationshilfen
readme.install und readme.maintain
sowie den Header-File clapack.h
stellt eine auf C++ basierende objektorientierte Schnittstelle zu LAPACK
dar. Der Sourcecode heißt lapack++.tgz und enthält in
komprimierter Form 66 kByte. Genauere Information über dieses System
sind in den folgenden Postcript-Files zu finden:
overview.ps classref.ps install.ps user.ps
Eine weitere interessante Internet-Adresse zum Thema LAPACK++:
http://math.nist.gov/lapack++
Anwendung von verteilten und parallelen Rechnersystemen zur Lösung
von Gleichungssystemen, Ausgleichsproblemen und Eigenwertproblemen
mit sehr großen Koeffizientenmatrizen (![]() ).
).
Eine kurze und prägnante Einführung in dieses Thema (Stand: 1995)
s. [22], S. 283-286.
Mathematica erlaubt sowohl symbolische als auch numerische Behandlung wichtiger Probleme der Linearen Algebra, wie z.B.:
Inverse[m] Matrix-Inversion
Det[m] Determinante
LinearSolve[m,b] Lösung des inhomogenen linearen Systems.
MATLAB:2.3 im Prinzip bietet diese Benutzersoftware die einfachste Realisierung der Lösung des linearen Gleichungssystems A.x=f :
>>% Eingabe der Koeffizientenmatrix A: >> A=[ ... ; ... ]; >>% Eingabe des inhomogenen Vektors f: >> f=[ ... ], >>% Loesung des Gleichungssystems: >> x=A\f
Eine alternative Lösungsmöglichkeit bietet Matlab durch folgende Befehle:
>>% Der inhomogene Vektor wird zur Koeffizientenmatrix als letzte Spalte >>% hinzugefuegt: >> Aplus=[A f]; >>% Diese erweiterte Matrix wird als Argument der Funktion rref >>% verwendet. Nun wird die urspruengliche Matrix mittels des Verfahrens >>% von Gauss-Jacobi in eine Einheitsmatrix umgewandelt, und die letzte >>% Spalte enthaelt den Loesungsvektor: >> Aneu=rref(Aplus); >> x=Aneu(:,end) >>% Dieses Verfahren hat den Vorteil, dass es etwas stabiler gegenueber >>% Rundungsfehlern ist als die obige "einfache" Loesung.
Diese NETLIB-Library enthält eine Reihe von Programmpaketen mit iterativen Lösungsmethoden für lineare Gleichungssysteme:
| Dateiname | Inhalt der Datei |
| sctemplates.tgz | C-Routinen, einfache Genauigkeit |
| dctemplates.tgz | C-Routinen, doppelte Genauigkeit |
| cpptemplates.tgz | C++-Routinen |
| sftemplates.tgz | F77-Routinen, einfache Genauigkeit |
| dftemplates.tgz | F77-Routinen, doppelte Genauigkeit |
| mltemplates.tgz | Matlab-Routinen |
Eine interessante Matlab-Routine ist sor.m. Dieses Programm löst ein lineares Gleichungssystem mittels der Sukzessiven Überrelaxationsmethode (allerdings ohne Berücksichtigung einer eventuellen Bandstruktur der Koeffizientenmatrix).