Nächste Seite: Numerische Integration Aufwärts: Numerische Methoden in der Vorherige Seite: Least-Squares Approximation
Gegeben sei eine reellwertige Funktion ![]() . Gesucht seien jene reellen
Werte von
. Gesucht seien jene reellen
Werte von ![]() , für welche die Gleichung
, für welche die Gleichung
Aus der Fülle der in der Literatur beschriebenen Methoden sollen in diesem Kapitel die folgenden Verfahren behandelt werden:
Anmerkung: Die Betonung auf transzendente Gleichungen im
Titel dieses Kapitels schließt natürlich die Behandlung algebraischer
Gleichungen vom Typus
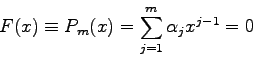
Die Gleichung ![]() kann immer (und fast immer auf mehrere Arten) auf die
Form
kann immer (und fast immer auf mehrere Arten) auf die
Form
Im Falle einer Konvergenz führt eine solche Iteration beliebig genau (bis
auf Rundungsfehler) an die exakte Lösung des Problems heran. Es gilt
Ein solches Konvergenzverhalten ist jedoch keineswegs selbstverständlich, sondern hängt sehr von der Art der Umformung von (5.1) in (5.2) ab, wie im folgenden Beispiel demonstriert werden soll.
Gesucht ist die Nullstelle der Funktion
![]() in der Umgebung
von 2. Es soll nun gezeigt werden, wie verschieden das Konvergenzverhalten
ist, wenn die Umformung auf (5.2) auf verschiedene Weise erfolgt:
in der Umgebung
von 2. Es soll nun gezeigt werden, wie verschieden das Konvergenzverhalten
ist, wenn die Umformung auf (5.2) auf verschiedene Weise erfolgt:
x0 = 2.0
t (a) (b) (c)
-----------------------------------------
0 2 2 2
1 3 1.6667 1.9129
2 22 2.8125 1.9050
3 10643 0.7236 1.9042
4 . -10.4944 1.9042
. . . .
. . . .
DIV DIV KONV
(b) zeigt ein interessantes Verhalten: s. Demo in der Vorlesung!
Um die Bedingung zu erhalten, unter der eine Konvergenz der Iteration
gewährleistet ist, geht man von der Gleichung (5.2) für die exakte
Lösung
![\begin{displaymath}\frac{f(x_{exakt})-f(x_{t})}{x_{exakt}-x_{t}} = f'(\xi_{t}) \quad \mbox{mit}
\quad \xi_{t}\in [x_{t},x_{exakt}] \quad . \end{displaymath}](img836.gif)
Somit ergibt sich weiters
Diese Gleichung kann Schritt für Schritt reduziert werden zu
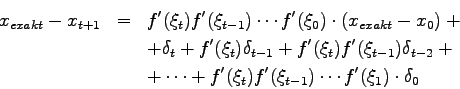
Für eine Fehlerabschätzung soll nun angenommen werden, daß
Dann ergibt sich
Der Grenzwert dieses Ausdruckes lautet:
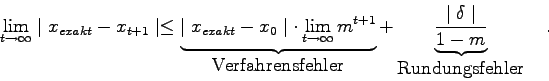
Beide Terme divergieren für ![]() , d.h. das Konvergenzkriterium
für die Iteration lautet:
, d.h. das Konvergenzkriterium
für die Iteration lautet:
Ist diese Bedingung erfüllt, ergibt sich
Was nun die Möglichkeiten betrifft, die auftretenden Fehler abzuschätzen, kann man wieder von der Gleichung (5.6) ausgehen:
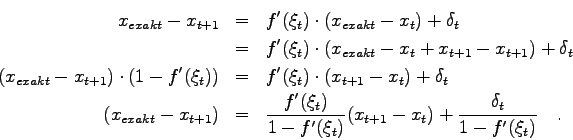
In der Praxis ist jedoch die Bestimmung von ![]() und
und ![]() meistens nicht
möglich oder zu kompliziert. Dann behilft man sich mit der stark
vereinfachten Fehlerabschätzung
meistens nicht
möglich oder zu kompliziert. Dann behilft man sich mit der stark
vereinfachten Fehlerabschätzung
=13cm
Abbruchbedingung.![]() x(t+1)-x(t)
x(t+1)-x(t)![]()
![]() EPSEnde der Iterationnaechster Iterationsschritt
für die Iteration ergibt.
EPSEnde der Iterationnaechster Iterationsschritt
für die Iteration ergibt.
Es muß aber ausdrücklich darauf hingewiesen werden, daß (5.11)
nur
für ![]() gilt, hingegen für
gilt, hingegen für ![]() grob falsch sein kann!
Außerdem ist (5.11) nur solange nützlich, als der
Verfahrensfehler größer ist als der Rundungsfehler!
grob falsch sein kann!
Außerdem ist (5.11) nur solange nützlich, als der
Verfahrensfehler größer ist als der Rundungsfehler!
Das folgende Beispiel soll einige der eben besprochenen Zusammenhänge illustrieren:
Die Funktion, deren Nullstelle numerisch ermittelt werden soll, lautet
Die erste Ableitung von ![]() hat an der Stelle
hat an der Stelle ![]() den Wert
den Wert
![]() . Dies ist gleichzeitig der Maximalwert der Ableitung im
Iterationsbereich, d. h. es gilt
. Dies ist gleichzeitig der Maximalwert der Ableitung im
Iterationsbereich, d. h. es gilt
Ergebnisse dieser Testrechnung:
.
Parameter a = 2.500 > 1.5 d.h. Divergenz ist zu erwarten:
t x_{t} x_{ex}-x_{t+1} x_{t+1}-x_{t}
0 .1200000E+01
1 .3400000E+00 .6600000E+00 -.8600000E+00
2 .2326600E+01 -.1326600E+01 .1986600E+01
3 -.5619601E+01 .6619601E+01 -.7946201E+01
4 -.4486988E+02 .4586988E+02 -.3925028E+02
5 -.3017459E+04 .3018459E+04 -.2972589E+04
6 -.1365759E+08 .1365759E+08 -.1365457E+08
7 -.2797945E+15 .2797945E+15 -.2797945E+15
8 -.1174274E+30 .1174274E+30 -.1174274E+30
9 -.2068380E+59 .2068380E+59 -.2068380E+59
10 -.6417295+117 .6417295+117 -.6417295+117
.
Parameter a = 0.600 ===> m=0.8 d.h.: Konvergenz, aber
Versagen von (5.11):
t x_{t} x_{ex}-x_{t+1} x_{t+1}-x_{t}
0 .6000000E+00
1 .7440000E+00 .2560000E+00 .1440000E+00
2 .8214144E+00 .1785856E+00 .7741440E-01
3 .8698886E+00 .1301114E+00 .4847425E-01
4 .9026825E+00 .9731750E-01 .3279386E-01
5 .9259343E+00 .7406572E-01 .2325178E-01
6 .9429417E+00 .5705828E-01 .1700744E-01
7 .9556556E+00 .4434437E-01 .1271392E-01
8 .9653111E+00 .3468892E-01 .9655443E-02
9 .9727302E+00 .2726981E-01 .7419114E-02
10 .9784816E+00 .2151839E-01 .5751419E-02
Parameter a = 1.200 ===> m=0.4 d.h.: Konvergenz und
Gueltigkeit von (5.11):
0 .6000000E+00
1 .1128000E+01 -.1280000E+00 .5280000E+00
2 .9455232E+00 .5447680E-01 -.1824768E+00
3 .1021197E+01 -.2119718E-01 .7567398E-01
4 .9914313E+00 .8568734E-02 -.2976591E-01
5 .1003413E+01 -.3412809E-02 .1198154E-01
6 .9986325E+00 .1367453E-02 -.4780262E-02
7 .1000547E+01 -.5466072E-03 .1914060E-02
8 .9997813E+00 .2187027E-03 -.7653099E-03
9 .1000087E+01 -.8747150E-04 .3061742E-03
10 .9999650E+00 .3499013E-04 -.1224616E-03
Im Abschnitt 5.2.1 wurde darauf hingewiesen, daß es gewöhnlich mehrere
Arten gibt, die Gleichung ![]() auf die äquivalente Form
auf die äquivalente Form ![]() zu
bringen.
Eine sehr wichtige Umformung ist gegeben durch
zu
bringen.
Eine sehr wichtige Umformung ist gegeben durch
Für die Fehlerabschätzung gilt wieder (5.10), wobei aber
![]() gemäß (5.9, 5.12) die konkrete Form
gemäß (5.9, 5.12) die konkrete Form
![\begin{displaymath}m = \mbox{max}_I \frac{d}{dx}\left(x-\frac{F(x)}{F'(x)}\rig...
...,x_{exakt}]} \left( \frac{F(x) F''(x)}{[F'(x)]^{2}}
\right)
\end{displaymath}](img865.gif)
Wenn aber die Newton-Raphson-Methode funktioniert, dann konvergiert sie sehr schnell, wie die folgende Rechnung demonstrieren soll:
Entwickelt man die Funktion ![]() an der Stelle
an der Stelle ![]() in eine Taylorreihe
bis zum (einschließlich) dritten Term, so ergibt sich
in eine Taylorreihe
bis zum (einschließlich) dritten Term, so ergibt sich
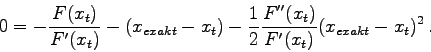

Eine Möglichkeit, mit eng nebeneinander liegenden Nullstellen-Paaren fertigzuwerden, ist die
Im allgemeinen bereitet es keine Schwierigkeiten, das Minimum oder Maximum
zwischen den beiden Nullstellen ![]() und
und ![]() zu lokalisieren. Nimmt man
an, der Abszissenwert des Extremums,
zu lokalisieren. Nimmt man
an, der Abszissenwert des Extremums, ![]() , sei hinlänglich genau bekannt, so
kann man
, sei hinlänglich genau bekannt, so
kann man ![]() an der Stelle
an der Stelle ![]() in eine Taylorreihe entwickeln:
in eine Taylorreihe entwickeln:
Quelle: [9],S. 257f mit Änderungen.
Das Funktions-Unterprogramm RTNEWT (RooT NEWTon) berechnet innerhalb eines gegebenen Intervalls eine reelle Nullstelle mittels der Newton-Raphson-Iteration.
INPUT-Parameter:
OUTPUT-Parameter:
Interne Variable:
Anmerkungen:
=15cm
Struktogramm 14FUNCTION RTNEWT(X1,X2,JMAX,
![]() XACC,FEHLER)X:=0.5*(X1+X2)(FUNC(X1,DF)*FUNC(X2,DF))
XACC,FEHLER)X:=0.5*(X1+X2)(FUNC(X1,DF)*FUNC(X2,DF)) ![]() 0.0FEHLER:=1
0.0FEHLER:=1
RTNEWT:=X
print:ERR(1) 'no zero in interval'
(return)......FEHLER:=2
J:=0DX:=FUNC(X,DF)/DF
X:=X-DX(X1-X)*(X-X2) ![]() 0.0FEHLER:=3
0.0FEHLER:=3![]() DX/X
DX/X![]()
![]() XACCFEHLER:=0......J:=J+1J
XACCFEHLER:=0......J:=J+1J![]() JMAX .or. FEHLER
JMAX .or. FEHLER![]() 2FEHLER=2print: 'ERR(2): no convergence'......
FEHLER=3print: 'ERR(3): jumped out of brackets'......RTNEWT:=X(return)
2FEHLER=2print: 'ERR(2): no convergence'......
FEHLER=3print: 'ERR(3): jumped out of brackets'......RTNEWT:=X(return)
Im allgemeinen hat die gegebene Funktion ![]() mehr als eine reelle
Nullstelle. In solchen Fällen ist es vernünftig, die
Newton-Raphson-Iteration
mit einer sogenannten 'Grob-Suche' zu kombinieren.
mehr als eine reelle
Nullstelle. In solchen Fällen ist es vernünftig, die
Newton-Raphson-Iteration
mit einer sogenannten 'Grob-Suche' zu kombinieren.
Das Prinzip dieser einfachen Strategie ist in der Abb. 5.7
dargestellt: die x-Achse wird in Schritten der Breite ![]() auf einen
Vorzeichenwechsel der Funktion
auf einen
Vorzeichenwechsel der Funktion ![]() untersucht. Wenn ein Intervall mit
der Eigenschaft
untersucht. Wenn ein Intervall mit
der Eigenschaft
![]() auftritt, so befindet sich in
auftritt, so befindet sich in
![]() (mindestens) eine Nullstelle, und die
Newton-Iteration kann beginnen.
(mindestens) eine Nullstelle, und die
Newton-Iteration kann beginnen.
Solch eine 'Grob-Suche' ist auch Teil des in Abschnitt 5.5 behandelten
Intervallschachtelungsverfahrens.
Es folgt nun ein Anwendungsbeispiel in C:
#include <stdio.h>
#include <math.h>
double func(double x,double *df)
// Diese Funktion berechnet die Funktionswerte sowie
// die Werte der ersten Ableitung fuer das Testbeispiel 5.3.3
{
*df=4*pow(x,3)-27*pow(x,2)-4*x+120;
return pow(x,4)-9*pow(x,3)-2*pow(x,2)+120*x-130;
}
double rtnewt(double x1, double x2, int jmax, double xacc, int *fehler)
// Diese Funktion bestimmt die reelle Nullstelle der Funktion 'func'
// im Intervall [x1,x2] mit der relativen Genauigkeit 'xacc'.
// Nach Beendigung der Rechnung kann die Variable 'fehler' einen der
// folgenden Werte haben:
// fehler=0 Die Newton-Raphson Iteration ist ok.
// fehler=1 Kein Vorzeichenwechsel der Funktion 'func'
// im Intervall [x1,x2].
// fehler=2 Keine Konvergenz waehrend 'jmax' Iter.schritten.
// fehler=3 Waehrend der Iteration springt der x Wert
// aus dem Intervall [x1,x2].
{
int j,pause;
double x,df,dx;
x=0.5*(x1+x2);
if((func(x1,&df)*func(x2,&df)) > 0.0) {
*fehler=1;
printf("ERROR(1): kein Vorzeichenwechsel in [x1,x2]\n");
return x;
}
*fehler=2;
j=0;
do {
dx=func(x,&df)/df;
x=x-dx;
if(((x1-x)*(x-x2))<0.0) *fehler=3;
else {
if(fabs(dx/x) < xacc) *fehler=0;
}
j++;
} while ((j<=jmax) && (*fehler==2));
if(*fehler==2)printf("ERROR(2): keine Konvergenz\n");
if(*fehler==3)printf("ERROR(3): x aus [x1,x2] gesprungen\n");
return x;
}
// ****** main program ******
void main()
{
int jmax,fehler,pause;
double a,b,hgrob,eps,xl,xr,yl,yr,df,zero;
// Parameter fuer die Grobsuche:
a=-10.0; b=10.0; hgrob=0.5;
// Parameter fuer die Newton-Raphson-Iteration:
jmax=20;
eps=0.0000001;
printf("TEST: NEWTON-RAPHSON-ITERATION MIT GROBSUCHE\n");
printf("\n Grobsuch-Bereich: %7.3f bis %7.3f\n",a,b);
printf(" Schrittweite Grobsuche: %7.3f\n",hgrob);
printf(" Par. fuer Newton: rel. Genauigkeit = %12.10f\n", eps);
printf(" max. Iter.schritte = %4i\n\n", jmax);
// Grobsuche:
xl=a;
yl=func(xl,&df);
xr=a+hgrob;
yr=func(xr,&df);
do {
if(yl*yr < 0.0) {
// Grobsuche hat Vorzeichenwechsel gefunden; Newton-Iteration wird gestartet:
zero=rtnewt(xl,xr,jmax,eps,&fehler);
if(fehler==0)
printf(" Nullstelle = %9.6f\n",zero);
else printf(" fehler(%1i) in RTNEWT\n",fehler);
}
xl=xr;
yl=yr;
xr=xl+hgrob;
yr=func(xr,&df);
} while(xl <= b);
printf("\nRechnung beendet.\n");
}
*********************************************
TEST: NEWTON-RAPHSON-ITERATION MIT GROBSUCHE
*********************************************
Grobsuch-Bereich: -10.000 bis 10.000
Schrittweite Grobsuche: 0.500
Par. fuer Newton: rel. Genauigkeit = 0.0000001000
max. Iter.schritte = 20
Nullstelle = -3.600135
Nullstelle = 1.228589
Nullstelle = 3.972068
Nullstelle = 7.399477
Rechnung beendet.
Diese mit dem Newton-Raphson-Verfahren nahe verwandte Methode wird häufig
dann verwendet, wenn die Berechnung der Ableitung der Funktion ![]() aus irgendwelchen Gründen Schwierigkeiten bereitet. In solchen Fällen kann
der Differentialquotient in (5.13) durch den
Differenzenquotienten ersetzt werden:
aus irgendwelchen Gründen Schwierigkeiten bereitet. In solchen Fällen kann
der Differentialquotient in (5.13) durch den
Differenzenquotienten ersetzt werden:
Um die rellen Nullstellen der Funktion ![]() in einem vorgegebenen
Intervall
in einem vorgegebenen
Intervall ![]() zu ermitteln, wird - ausgehend von
zu ermitteln, wird - ausgehend von ![]() - mit einer
vorgegebenen Schrittweite
- mit einer
vorgegebenen Schrittweite ![]() eine grobe Lokalisierung der Nullstellen
vorgenommen.
eine grobe Lokalisierung der Nullstellen
vorgenommen.
Angenommen, die erste Nullstelle befinde sich im Intervall
![]() (s. Abb.5.7). Dies wird daran erkannt, daß innerhalb dieses Intervalls
die Funktion
(s. Abb.5.7). Dies wird daran erkannt, daß innerhalb dieses Intervalls
die Funktion ![]() einen Vorzeichenwechsel hat, daß also gilt:
einen Vorzeichenwechsel hat, daß also gilt:
Es gibt nun drei Möglichkeiten:
Dieses einfache Algorithmus wird durch das folgende Beispiel verdeutlicht:
gesucht sei die Nullstelle von
![\includegraphics[scale=0.9]{num5_fig/intsch}](img42.png)
Es soll noch erwähnt werden, daß die Intervallschachtelungsmethode
zu jenen numerischen Verfahren gehört, bei denen - zumindest für den
absoluten Fehler - eine a priori Fehlerabschätzung
in der Form
Im Prinzip ist diese Methode sehr sicher. Ist eine Nullstelle erst einmal
im Intervall ![]() lokalisiert, so ist ihre Berechnung (abgesehen
von Rundungsfehlern) mit beliebiger Genauigkeit möglich. Es gibt also
keinerlei Konvergenzprobleme.
lokalisiert, so ist ihre Berechnung (abgesehen
von Rundungsfehlern) mit beliebiger Genauigkeit möglich. Es gibt also
keinerlei Konvergenzprobleme.
Die einzige Unsicherheitsquelle liegt in der Wahl der
Schrittweite h für die Grobsuche.
Das Kriterium: Vorzeichenwechsel ![]() Nullstelle ist nämlich
keinesfalls unproblematisch (s. Abb. 5.9):
Nullstelle ist nämlich
keinesfalls unproblematisch (s. Abb. 5.9):
In beiden Fällen ist also die Anfangs-Schrittweite ![]() zu groß gewählt
worden!
zu groß gewählt
worden! ![]() stellt also die Auflösungsgrenze des Verfahrens dar:
stellt also die Auflösungsgrenze des Verfahrens dar:
Es können (im allgemeinen) nur solche Nullstellen gefunden werden,
deren Abstand nicht kleiner ist als die Anfangs-Schrittweite ![]() .
.
Quelle: [2],S.281f mit einigen Änderungen und Vereinfachungen.
INPUT-Parameter:
OUTPUT-Parameter:
Fehlerdiagnostik:
ANZ=0: es wurden keine Nullstellen gefunden.
ANZ=ANZMAX+1: es wurden mehr als ANZMAX Nullstellen gefunden,
aber nur die ANZMAX ersten Nullstellen wurden im Feld NULLST abgespeichert.
allgemeine Anmerkung:
Das im folgenden präsentierte Programm ist gegenüber der Quelle
deutlich vereinfacht; insbesondere ist der Fall nicht
berücksichtigt, daß eine Nullstelle exakt auf einer
Intervallgrenze liegt.
Anmerkung zur Fehlerabfrage:
Im Programm INTSCH wird standardmäßig eine relative Fehlerabfrage
durchgeführt. Nur wenn die Nullstelle sehr klein ist (dem Betrage nach
kleiner als 10![]() ), wird auf eine absolute Fehlerabfrage umgeschaltet.
), wird auf eine absolute Fehlerabfrage umgeschaltet.
=16cm
Struktogramm 15INTSCH(ANF,AEND,H,GEN,ANZMAX,NULLST,ANZ)EPS:=1.e-8
ANZ:=0
XL:=ANF
YL:=FCT(XL)XR:=XL+H
YR:=FCT(XR)YL*YR ![]() 0.0XL:=XR
0.0XL:=XR
YL:=YRANZ:=ANZ+1ANZ ![]() ANZMAXprint:'zu viele
ANZMAXprint:'zu viele
Nullstellen'
(return)SPEICH:=XR
X:=(XL+XR)/2.0
Y:=FCT(X)YL*Y ![]() 0.0XR:=X
0.0XR:=X
YR:=YXL:=X
YL:=Y![]() X
X![]()
![]() EPSERROR:=XR-XLERROR:=(XR-XL)/
EPSERROR:=XR-XLERROR:=(XR-XL)/![]() X
X![]() ERROR
ERROR ![]() GENNULLST(ANZ):=(XR+XL)/2.0
GENNULLST(ANZ):=(XR+XL)/2.0
XL:=SPEICH
YL:=FCT(XL)XL+H ![]() AEND(return)
AEND(return)
Die reellen Nullstellen der algebraischen Gleichung
INTSCH liefert die folgenden vier Nullstellen:
.
1 -3.600135
2 1.228589
3 3.972068
4 7.399477
Dieses Ergebnis ist natürlich exakt dasselbe wie bei der Newton-Iteration
(vgl. Abschnitt 5.3.3). Es ist hier interessant, den Aufwand zu untersuchen,
den beide Methoden benötigen, um ein Ergebnis dieser Genauigkeit zu
erzielen.
Wenn man die Anzahl der Funktionsaufrufe von 'func'
(im Newton-Raphson-Programm) abzählt, kommt man auf 66 Aufrufe; die gleiche
Analyse für das Intervallschachtelungsprogramm ergibt 131 Aufrufe von
'fct'. Da aber beim Newton-Verfahren bei jedem Aufruf von 'func' 2 Funktionen
berechnet werden, nämlich der Funktionswert sowie der Wert der ersten
Ableitung, ist der numerische Aufwand in beiden Programmen etwa gleich.
Diese Analyse gibt allerdings ein falsches Bild von der Leistungsfähigkeit
der Newton-Raphson-Iteration. Ein großer Teil der Funktionsaufrufe von
'func' geschieht bei der Grobsuche, bei der die Berechnung der Ableitungen
unnötig ist! Es wäre daher ökonomischer, beim Newton-Raphson-Verfahren
zwei unabhängige Funktionen (z.B. 'func' und 'dfunc') zu definieren, wobei
'func' nur die Funktion und 'dfunc' nur die Ableitung berechnet.
Geht man so vor, ergeben sich bei der Anwendung des Programms
RTNEWT
auf das Testproblem nur mehr 66 Aufrufe von 'func' und 15 Aufrufe von 'dfunc',
also insgesamt 81 Funktionsaufrufe.
D.h.: Je ökonomischer man die Grobsuche gestaltet, desto stärker wird die Überlegenheit der Newton-Iteration gegenüber der Intervallschachtelung deutlich. Betrachten Sie etwa die erste Nullstelle: sie liegt im 'Grobsuch-Intervall' [-4.0, -3.5]. Im folgenden sehen Sie die weitere Annäherung an die Nullstelle, links mittels Newton-Raphson und rechts mittels Intervallschachtelung:
Newton-Raphson Int.schachtelung
-3.750000 -3.750000
-3.609011 -3.625000
-3.600169 -3.562500
-3.600135 -3.593750
-3.600135 -3.609375
-3.601562
-3.597656
-3.599609
-3.600586
-3.600098
-3.600342
-3.600220
-3.600159
-3.600128
-3.600143
-3.600136
-3.600132
-3.600134
-3.600135
-3.600135
-3.600135
-3.600135
Ein Vorteil der Intervallschachtelungsmethode gegenüber Newton-Raphson
besteht
natürlich darin, daß erstere keine Ableitungen der Funktion ![]() benötigt! Diesen Vorteil teilt sie mit der im Abschnitt 5.4 kurz
beschriebenen Regula Falsi.
benötigt! Diesen Vorteil teilt sie mit der im Abschnitt 5.4 kurz
beschriebenen Regula Falsi.
Im folgenden Beispiel geht es um die Energie-Eigenwerte eines eindimensionalen Potentialtopfes:
Gesucht sind jene Energiewerte ![]() , die ein Teilchen der Masse
, die ein Teilchen der Masse ![]() unter dem
Einfluß des Kastenpotentials (s.Abb.5.10)
unter dem
Einfluß des Kastenpotentials (s.Abb.5.10)
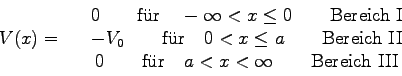
Zu lösen ist also die eindimensionale Schrödingergleichung
Lösungsansätze:
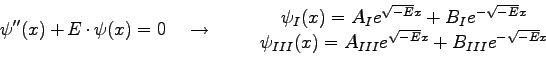
Die Randbedingungen sind nur für
![]() erfüllt, und man erhält:
erfüllt, und man erhält:
Zusätzlich sind noch die 4 Anschlußbedingungen
(Abkürzung:
![]() ).
).
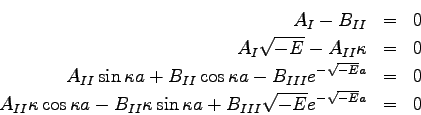
Die Nullstellensuche für beliebige ![]() und
und ![]() soll mittels der
Intervallschachtelungs-Methode durchgeführt werden. Diese ist im konkreten Fall
der Newton-Raphson-Iteration vorzuziehen, weil man sich dadurch die
Berechnung der Ableitung der Funktion
soll mittels der
Intervallschachtelungs-Methode durchgeführt werden. Diese ist im konkreten Fall
der Newton-Raphson-Iteration vorzuziehen, weil man sich dadurch die
Berechnung der Ableitung der Funktion ![]() erspart.
erspart.
Ergebnis für einen Potentialtopf mit ![]() Bohr und
Bohr und
![]() Rydberg:
Rydberg:
.
Es wurden 10 Energiewerte mit der rel. Genauigkeit von 0.000001
ermittelt:
1 Energie [Ry] = -222.83185
2 Energie [Ry] = -216.33258
3 Energie [Ry] = -205.51910
4 Energie [Ry] = -190.42145
5 Energie [Ry] = -171.08820
6 Energie [Ry] = -147.59515
7 Energie [Ry] = -120.06418
8 Energie [Ry] = -88.70779
9 Energie [Ry] = -53.96208
10 Energie [Ry] = -17.15278
Probleme dieser Art sollen hier nur prinzipiell erläutert werden, weil sie sich - wie sogleich gezeigt wird - mittels des bereits ausführlich behandelten Gauss-Newton-Marquardt-Verfahrens numerisch lösen lassen.
Hat man nämlich anstatt einer einzelnen Gleichung ![]() ein
System von
ein
System von ![]() nicht-linearen Gleichungen mit den
nicht-linearen Gleichungen mit den ![]() Unbekannten
Unbekannten
![]() ,
, ![]() ,
,![]() ,
, ![]() vorliegen, also
vorliegen, also
![\begin{displaymath}S = \sum_{k=1}^{n} [F_{k}(x_{1},x_{2},\ldots,x_{n})]^{2} = 0 \end{displaymath}](img948.gif)
In diesem Fall ist also Null das anzustrebende Minimum der Summe ![]() , und
gesucht wird jener Vektor (werden jene Vektoren)
, und
gesucht wird jener Vektor (werden jene Vektoren) ![]() , der (die)
dies bewerkstelligt (bewerkstelligen)!
, der (die)
dies bewerkstelligt (bewerkstelligen)!
Damit ist das Problem (5.23) auf ein spezielles nicht-lineares Least-Squares-Problem zurückgeführt, und man kann das Gauss-Newton-Marquardt-Verfahren (s. Kap. 4) anwenden:
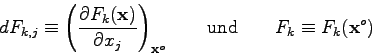
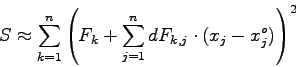
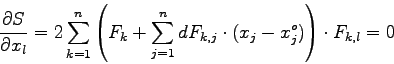
Vergleicht man nun das System (5.26) mit dem System (4.20), so ist die nahe Verwandtschaft sofort evident. Auch zur Lösung von (5.26) ist es sehr zu empfehlen, die 'Marquardt-Variation' zu verwenden, um eine hohe Konvergenz-Sicherheit der Iteration zu erhalten.
Man löse das Gleichungssystem5.1
Exakte Lösungen:
(![]() ,
, ![]() ) (
) (![]() ,
, ![]() )
(
)
(![]() ,
,
![]() )
)
Numerische Lösung mittels der Gauss-Newton-Marquardt-Methode:
.
abs. Gen. der Fitwerte = .100000E-06
tmax = 50
guessed values: x(1) = -.2000000E+00
x(2) = -.5000000E+00
0 .740389E+00 -.200000E+00 -.500000E+00
*
*
*
*
*
1 .100543E+00 -.595187E+00 -.823118E+00
2 .374490E-02 -.513359E+00 -.850427E+00
3 .478015E-05 -.500104E+00 -.865304E+00
4 .227994E-09 -.500000E+00 -.866020E+00
5 .543610E-15 -.500000E+00 -.866025E+00
6 .543610E-15 -.500000E+00 -.866025E+00
Ergebnisse mittels MRQMIN und MRQCOF:
=====================================
x(1) = -.50000E+00 (exakt: -0.5000000)
x(2) = -.86603E+00 (exakt: -0.8660254)
Anmerkung: Wie bei iterativen Methoden in der Anwendung auf nicht-lineare Probleme üblich, hängt es von den Startwerten des GNM-Prozesses ab, welche der drei Lösungen man erhält. Mit den oben gewählten Startwerten bekommt man offenbar die dritte Lösung.
Die erste Lösung würde man z.B. für die Startwerte ![]() =-1.0 und
=-1.0 und
![]() =0.0 erhalten, die zweite Lösung für die Startwerte
=0.0 erhalten, die zweite Lösung für die Startwerte
![]() =-1.0 und
=-1.0 und ![]() =1.0.
=1.0.
fnewton.c newpsz.f90 Newtonverfahren fuer reelle Funktionen
fpegasus.c pegasu.f90 Pegasusverfahren fuer reelle Funktionen
froots.c Pegasus-, Pegasus-King-, Anderson-Bjoerck-
und Anderson-Bjoerck-King-Verfahren
fzeroin.c zeroin.f90 Zeroin-Verfahren fuer reelle Funktionen
fmueller.c muller.f90 Verfahren von Mueller zur Berechnung aller
Nullstellen eines reellen Polynoms
fbauhube.c baupol.f90 Verfahren von Bauhuber zur Berechnung aller
Nullstellen eines komplexen Polynoms
flaguer.c laguer.f90 Verfahren von Laguerre zur Berechnung aller
reellen Nullstellen eines reellen Polynoms
roots.m Berechnung der Nullstellen eines Polynoms,
wobei das Funktionsargument die Koeffizienten
des Polynmos sind.
fzero.m Berechnung der Nullstelle einer Funktion F(x)
in der Naehe eines Anfangswertes x0.