Nächste Seite: Eigenwerte und Eigenvektoren reeller Aufwärts: Numerische Methoden in der Vorherige Seite: Numerische Lösung von transzendenten
In diesem Kapitel geht es um die numerische Auswertung von bestimmten
Integralen
Numerische Methoden kommen dann zur Anwendung, wenn
Angenommen, eine zu integrierende Funktion ![]() sei nur bzgl. der
sei nur bzgl. der ![]() Stützpunkte
Stützpunkte
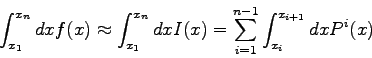
![\begin{displaymath}= \sum_{i=1}^{n-1} \int_{x_{i}}^{x_{i+1}} dx \left[
a_{i} + b_{i}(x-x_{i})+c_{i}(x-x_{i})^{2}+d_{i}(x-x_{i})^{3} \right] \end{displaymath}](img971.gif)
Für alle weiteren Ausführungen soll gelten: die (reellwertige)
Integrandenfunktion ![]() ist analytisch gegeben und im gesamten
Integrationsintervall
ist analytisch gegeben und im gesamten
Integrationsintervall ![]() stetig.
stetig.
besteht in der näherungsweisen Berechnung von bestimmten Integralen mit Hilfe von sogenannten Quadraturformeln:
Die Differenz
Während der Grad der Quadraturformel, d.h. die Anzahl ![]() der Summenterme,
im Prinzip frei wählbar ist, müssen die Stützpunkte und die
Gewichtsfaktoren möglichst optimal gewählt werden. Im weiteren soll nun
eine Optimierungsvorschrift für diese Größen angegeben werden.
der Summenterme,
im Prinzip frei wählbar ist, müssen die Stützpunkte und die
Gewichtsfaktoren möglichst optimal gewählt werden. Im weiteren soll nun
eine Optimierungsvorschrift für diese Größen angegeben werden.
Für die Quadraturformel (6.2) ![]() -ten Grades gibt es offenbar
-ten Grades gibt es offenbar ![]() zu optimierende
Parameter. Bei zahlreichen Quadraturformeln wird jedoch diese Anzahl noch
durch zusätzliche einschränkende Bedingungen vermindert. Im
allgemeinen sind daher nur
zu optimierende
Parameter. Bei zahlreichen Quadraturformeln wird jedoch diese Anzahl noch
durch zusätzliche einschränkende Bedingungen vermindert. Im
allgemeinen sind daher nur
Man geht nun von einem allgemeinen Polynom vom Grade ![]() aus:
aus:
Die Trapezformel lautet somit
Der Name 'Trapezformel' hat geometrische Gründe (s. Abb. 6.1).
ist eine Quadraturformel dritten Grades, d.h.
Die Verfahrensfehler der Quadraturformeln (6.5) und (6.6)
können mittels Anwendung des Mittelwertsatzes der Integralrechnung
bestimmt werden. Sie lauten
Die Verfahrensfehler steigen also mit der 3. bzw. der 5. Potenz der Breite des Integrationsintervalls an. Das bedeutet natürlich, daß eine Anwendung von (6.5) bzw. (6.6) für größere Intervallbreiten zu vollkommen obsoleten Ergebnissen führt!
Die einzige Möglichkeit, mittels Trapez- und Simpsonformel zu brauchbaren
Ergebnissen zu kommen, ist eine
Aufteilung des gegebenen Intervalls ![]() in eine Reihe von
in eine Reihe von ![]() Subintervallen mit der Intervallbreite
Subintervallen mit der Intervallbreite ![]() :
:
![\includegraphics[scale=0.7]{num6_fig/aqua2}](img46.png)
![\begin{displaymath}Q^{ST}(f) = \sum_{i=1}^{N} \frac{h}{2} \left[ f(x_{i}) + f(x_{i+1}) \right]
\end{displaymath}](img1003.gif)
Ebenso kann man die Simpsonformel (6.6) auf jeweils 2
nebeneinander liegende Subintervalle anwenden, was voraussetzt, daß man
für ![]() eine gerade Zahl wählt.6.4Eine Summierung über die
eine gerade Zahl wählt.6.4Eine Summierung über die ![]() Teilergebnisse ergibt
Teilergebnisse ergibt
![\begin{displaymath}Q^{SS}(f)=\frac{h}{3} \left[ f(c) + 2\sum_{i=1}^{N/2-1} f(x_{2i+1}) +
4\sum_{i=1}^{N/2} f(x_{2i}) + f(d) \right] \end{displaymath}](img1006.gif)
Auch für die summierten Formeln (6.9) und (6.10) werden die
Verfahrensfehler ohne Ableitung angegeben:
Im allgemeinen wird man keine Information darüber haben, wieviele
Subintervalle in die Rechnung einbezogen werden müssen, um ein numerisches
Ergebnis der gewünschten Genauigkeit zu erhalten (eine a-priori
Fehlerabschätzung
auf Basis von (6.11) ist wegen der Unkenntnis
von ![]() nicht möglich). Man muß sich also an das gewünschte
Ergebnis 'herantasten', wobei man die Stützpunktanzahl sukzessive erhöht.
Am günstigsten ist es, die Stützpunktanzahl immer wieder zu verdoppeln
(s. Abb. 6.2).
nicht möglich). Man muß sich also an das gewünschte
Ergebnis 'herantasten', wobei man die Stützpunktanzahl sukzessive erhöht.
Am günstigsten ist es, die Stützpunktanzahl immer wieder zu verdoppeln
(s. Abb. 6.2).
Man geht dabei von der simpelsten Näherung aus, nämlich von zwei
Stützpunkten (![]() = 1 Intervall), und man erhält
= 1 Intervall), und man erhält
![\begin{displaymath}Q_{M=2}^{ST}=\frac{(d-c)}{2} \left[ \frac{1}{2} f(c)
+f\lef...
...M=1}^{ST} + (d-c)
f\left(\frac{c+d}{2}\right) \right] \quad . \end{displaymath}](img1016.gif)
Eine weitere Verdoppelung auf 4 Subintervalle erfordert lt. Abb. 6.2
die Berechnung von ![]() und
und ![]() :
:
![\begin{displaymath}Q_{M=4}^{ST}=\frac{1}{2} \left\{ Q_{M=2}^{ST} + \frac{(d-c)}{...
...+ f\left(c+\frac{3(d-c)}{4}\right)
\right] \right\} \quad .
\end{displaymath}](img1019.gif)
Offensichtlich gilt bei jeder Verdoppelung der Subintervalle die
Rekursionsformel
(6.13) bildet die Basis für die Programme QTRAP und TRAPZD im Abschnitt 6.5.
Durch die fortgesetzte Anwendung der Formel (6.13) erhält man also
eine Folge von Näherungswerten für ein bestimmtes Integral nach
Maßgabe der summierten Trapezformel:
Nun stellen sich die Fragen: 'Wie genau sind die erhaltenen numerischen Werte?' bzw. 'Wieviele Subintervall-Verdoppelungen sind nötig, um eine bestimmte vorgegebene (absolute oder relative) Genauigkeit zu erreichen?'.
Das Problem einer solchen internen Fehlerdiagnose liegt darin, daß während des Programmablaufes eine möglichst zuverlässige Fehlerabschätzung, basierend auf dem vorliegenden Datenmaterial, erfolgen muß. Dabei kann man z. B. wie folgt vorgehen:
Wenn man die Rundungsfehler im Moment außer Acht läßt, kann man
unter Verwendung von Glg. (6.11) und unter Berücksichtigung von
![]() schreiben:
schreiben:
Nimmt man nun an, daß näherungsweise
Daraus kann man Abbruchbedingungen für ein auf (6.13) beruhendes Programm gewinnen:
Die Rekursion (6.13) wird solange fortgesetzt, bis der
vorgegebene absolute oder relative Fehler GEN
unterschritten wird, also bis gilt:
Quelle: [9], S. 111ff mit Änderungen.
INPUT-Parameter:
OUTPUT-Parameter:
=16cm
Struktogramm 16QTRAP(C,D,JMAX,IREL,GEN,S,FEHLER) FEHLER:= TRUE JMAX ![]() 2JMAX:=2...... TRAPZD(C,D,S,1)OLDS:=S
2JMAX:=2...... TRAPZD(C,D,S,1)OLDS:=S
J:=2 TRAPZD(C,D,S,J) ERROR:=![]() S-OLDS
S-OLDS ![]() /3IREL=1ERROR:=ERROR/
/3IREL=1ERROR:=ERROR/![]() S
S ![]() ......ERROR
......ERROR ![]() GENFEHLER:=FALSEOLDS:=SJ:=J+1J
GENFEHLER:=FALSEOLDS:=SJ:=J+1J ![]() JMAX .or. notFEHLERJ
JMAX .or. notFEHLERJ ![]() JMAXprint: 'QTRAP Gen. nicht erreicht.'......(return)
JMAXprint: 'QTRAP Gen. nicht erreicht.'......(return)
Struktogramm 17TRAPZD(C,D,S,J)J=1
S:=0.5*(D-C)*(FUNC(C)+FUNC(D)) TNM:=2**(J-2)
DEL:=(D-C)/TNM
X:=C + 0.5*DEL
SUM:=0.0I=1(1)TNM SUM:=SUM + FUNC(X)
X:=X+DEL S:=0.5*(S+(D-C)*SUM/TNM)(return)
Anmerkung: Die Routine TRAPZD muß hintereinander für J=1,2,3,... aufgerufen werden.
Der folgende einfache Test soll Ihnen das korrekte Funktionieren
der Programme QTRAP und TRAPZD dokumentieren:
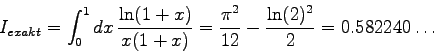
TEST FUER DIE ROUTINEN QTRAP UND TRAPZD
NUM. METHODEN IN DER PHYSIK WS 2000/2001 28-8-2000
H. Sormann F90 DOUBLE PRECISION
J Funkt. num. Erg. wahrer geschaetzter GEN
aufrufe abs. Fehler abs. Fehler
2 3 0.60695347 0.247129E-01 0.221111E-01 0.100000E-05
3 5 0.58858506 0.634453E-02 0.612280E-02 0.100000E-05
4 9 0.58383827 0.159774E-02 0.158226E-02 0.100000E-05
5 17 0.58264071 0.400184E-03 0.399185E-03 0.100000E-05
6 33 0.58234062 0.100093E-03 0.100030E-03 0.100000E-05
7 65 0.58226555 0.250263E-04 0.250223E-04 0.100000E-05
8 129 0.58224678 0.625675E-05 0.625651E-05 0.100000E-05
9 257 0.58224209 0.156420E-05 0.156418E-05 0.100000E-05
10 513 0.58224092 0.391051E-06 0.391050E-06 0.100000E-05
EXAKT = 0.5822405265
Ergebnis = 0.5822409175
geforderte Genauigkeit (abs) = 0.000001000
Dazu waren 513 Funktionsaufrufe noetig.
Wie aus den Gleichungen (6.11) und (6.12) für die
Verfahrensfehler
der summierten Trapezformel (Ordnung ![]() =2) und der summierten Simpsonformel
(Ordnung
=2) und der summierten Simpsonformel
(Ordnung ![]() =3) hervorgeht, sind diese gegeben durch
=3) hervorgeht, sind diese gegeben durch
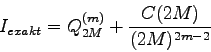
Man kann zeigen:
'![]() ' entspricht dem Ergebnis einer Quadraturformel mit
' entspricht dem Ergebnis einer Quadraturformel mit ![]() Subintervallen und einer um Eins höheren Ordnung:
Subintervallen und einer um Eins höheren Ordnung:
Verifikation der Glg. (6.19) durch ein Beispiel:
Geht man von der Trapezformel (![]() ) sowie von
zwei Subintervallen (
) sowie von
zwei Subintervallen (![]() ) aus, so erhält man
) aus, so erhält man
![\begin{displaymath}Q_{2}^{(2)} = \frac{(d-c)}{2} \left[ \frac{1}{2} f(c) +
f\left(\frac{c+d}{2}\right) + \frac{1}{2} f(d)
\right] \quad . \end{displaymath}](img1044.gif)
![\begin{displaymath}Q_{4}^{(2)}=\frac{(d-c)}{4} \left[ \frac{1}{2} f(c) +
f\lef...
...+3\frac{(d-c)}{4}\right) +
\frac{1}{2} f(d) \right] \quad .
\end{displaymath}](img1045.gif)
![\begin{displaymath}Q_{4}^{(3)}=\frac{(d-c)}{6} \left[ \frac{1}{2} f(c)
+2 f\le...
...+3\frac{(d-c)}{4}\right) +
\frac{1}{2} f(d) \right] \quad ,
\end{displaymath}](img1046.gif)
Man erhält also durch Anwendung der Formel (6.19) auf 2 Trapezformeln genau die Simpsonformel.
Die Strategie von Romberg, die auf der Gleichung (6.19) beruht, ist mit Hilfe des folgenden Schemas leicht zu verstehen:
![\includegraphics[scale=0.9]{num6_fig/romb}](img48.png)
Die Kleinbuchstaben links neben den Q-Symbolen bezeichnen die Reihenfolge
der Berechnung, und die zusammenlaufenden Pfeile bedeuten die Anwendung
von (6.19). D.h., von Zeile zu Zeile verdoppelt sich die Anzahl
der Subintervalle, von Spalte zu Spalte erhöht sich die Ordnung der
Quadraturformel.
Es ist nun plausibel anzunehmen, daß die
Diagonalelemente des obigen Schemas schneller zum gewünschten
Integralwert konvergieren als die Zeilen- und Spaltenelemente,
weil ja entlang der Diagonale sowohl die Subintervall-Zahl als auch die
Ordnung der Quadratur erhöht werden.
Man kann in der Tat zeigen, daß für viele praktische Anwendungen
der Romberg-Strategie
die Differenz zwischen zwei aufeinanderfolgenden Diagonalelementen
des Romberg-Schemas eine gute Näherung für den absoluten Fehler des
Elementes ![]() darstellt.
darstellt.
Diese Fehlerabschätzung hat aber eine unschöne Seite: man muß
offensichtlich, um die Genauigkeit des Diagonalelementes des Zeile ![]() bestimmen zu können, die gesamte folgende Zeile
bestimmen zu können, die gesamte folgende Zeile ![]() berechnen!
berechnen!
Quellen: [9], S. 114f, [2], S. 205ff und 407f, mit Änderungen.
Das Programm ROMB berechnet einen Näherungswert für ein bestimmtes Integral.
INPUT-Parameter:
OUTPUT-Parameter:
Das Programm ROMB benötigt die bereits besprochene Routine TRAPZD.
Anmerkung: Was die Leistungsfähigkeit des Romberg-Verfahrens betrifft, so ist (frei zitiert nach [9], S. 115) ... die Romberg-Routine sehr leistungsfähig für genügend glatte Integranden ... Unter solchen Umständen braucht das Programm ROMB viel, viel weniger Funktionsaufrufe als jedes andere Programm, das auf der Trapez- oder der Simpsonformel beruht.
=16cm
Struktogramm 18:ROMB(C,D,KMIN,KMAX,IREL,GEN,S,ERROR,FEHLER) FEHLER:=TRUE KMAX ![]() 3 KMAX:=3...... TRAPZD(C,D,Q(2),1) K:=3 M=2(1)K-1 QALT(M):=Q(M) TRAPZD(C,D,Q(2),K-1) FAC:=1 M=2(1)K-1 FAC:=FAC*K
3 KMAX:=3...... TRAPZD(C,D,Q(2),1) K:=3 M=2(1)K-1 QALT(M):=Q(M) TRAPZD(C,D,Q(2),K-1) FAC:=1 M=2(1)K-1 FAC:=FAC*K
Q(M+1):=(FAC*Q(M)-QALT(M))/(FAC-1) ERROR:=![]() QALT(K-1)-Q(K)
QALT(K-1)-Q(K) ![]() IREL = 1 ERROR:=ERROR/
IREL = 1 ERROR:=ERROR/![]() QALT(K-1)
QALT(K-1)![]() ...... K
...... K ![]() KMINERROR
KMINERROR ![]() GEN S:=QALT(K-1)
GEN S:=QALT(K-1)
FEHLER:=FALSE............ K:=K+1K ![]() KMAX .or. notFEHLERK
KMAX .or. notFEHLERK ![]() KMAXprint: 'ROMB Gen. nicht erreicht.'......(return)
KMAXprint: 'ROMB Gen. nicht erreicht.'......(return)
Das folgende Output-Protokoll zeigt Ihnen an Hand des Beispiels von S. 169 die Überlegenheit des Romberg-Algorithmus gegenüber der Trapezmethode:
NUM. METH. IN DER PHYSIK WS 2000/2001 ROMBERG-FORMEL 28-8-2000
INTEGRAL Skriptum S. 169
H. Sormann F90 DOUBLE PRECISION
m Funkt. num. Erg. wahrer geschaetzter absGEN
aufrufe abs. Fehler abs. Fehler
2 3 0.67328680 0.910463E-01 0.884444E-01 0.100000E-05
3 5 0.58484236 0.260183E-02 0.253878E-02 0.100000E-05
4 9 0.58230358 0.630557E-04 0.623029E-04 0.100000E-05
5 17 0.58224128 0.752829E-06 0.749125E-06 0.100000E-05
EXAKT = 0.5822405265
Ergebnis = 0.5822412793
geforderte Gen. (abs) = 0.100000E-05
Dazu waren 17 Funktionsaufrufe noetig.
Das eben erläuterte Verfahren wird im folgenden auf Integrale vom Typus
In den folgenden Tests geht es hauptsächlich um die Zuverlässigkeit
der auf Glg. (6.20) basierenden Fehlerdiagnostik im Romberg-Programm.
Das Verhalten des absoluten Fehlers ist in den oberen Diagrammen
der Abbildungen 6.4 (für ![]() ) und 6.5 (für
) und 6.5 (für
![]() ) dargestellt.
) dargestellt.
![\includegraphics[scale=0.8]{num6_fig/aqua5a}](img50.png) |
![\includegraphics[scale=0.8]{num6_fig/aqua5b}](img51.png) |
Sowohl für den schwach (![]() ) als auch für den stark oszillierenden
Integranden (
) als auch für den stark oszillierenden
Integranden (![]() ) ist im Bereich
) ist im Bereich
![]() eine sehr gute
Übereinstimmung zwischen dem 'wahren' Fehler
und dem vom Programm geschätzten Fehler zu beobachten.
Die Kurven liegen praktisch aufeinander, und die
Fehler zwischen numerischer Näherung und exakter Lösung nehmen mit
fortschreitendem Romberg-Prozess (=mehr Stützpunkte, höhere Ordnung der
Quadraturformel) monoton ab. Auf diese Weise kann der absolute
Verfahrensfehler bis auf
eine sehr gute
Übereinstimmung zwischen dem 'wahren' Fehler
und dem vom Programm geschätzten Fehler zu beobachten.
Die Kurven liegen praktisch aufeinander, und die
Fehler zwischen numerischer Näherung und exakter Lösung nehmen mit
fortschreitendem Romberg-Prozess (=mehr Stützpunkte, höhere Ordnung der
Quadraturformel) monoton ab. Auf diese Weise kann der absolute
Verfahrensfehler bis auf
![]() reduziert werden.
Natürlich wird dieser Wert für den schwach oszillierenden Integranden
bedeutend früher erreicht (
reduziert werden.
Natürlich wird dieser Wert für den schwach oszillierenden Integranden
bedeutend früher erreicht (![]() ) als für den stark oszillierenden
Integranden (
) als für den stark oszillierenden
Integranden (![]() ).
).
Ab ![]() (für
(für ![]() ) bzw.
) bzw. ![]() (für
(für ![]() ) kann der Fehler des
numerischen Ergebnisses nicht mehr
weiter reduziert werden, er nimmt im Gegenteil sogar leicht zu!
Die Ursache dafür sind natürlich Rundungsfehler, die mit
Zunahme der Stützpunktzahl größer werden und bei einem gewissen
) kann der Fehler des
numerischen Ergebnisses nicht mehr
weiter reduziert werden, er nimmt im Gegenteil sogar leicht zu!
Die Ursache dafür sind natürlich Rundungsfehler, die mit
Zunahme der Stützpunktzahl größer werden und bei einem gewissen ![]() den Verfahrensfehler übersteigen.
den Verfahrensfehler übersteigen.
Man muß also beim Numerischen Integrieren (und nicht nur dort)
zur Kenntnis nehmen:
Auf Grund der Rundungsfehler kann die Genauigkeit einer numerischen
Integration nur bis zu einer gewissen Grenze gesteigert werden. Ab dieser
Grenze bringt eine weitere Erhöhung des Rechenaufwandes keine
Verbesserung der Ergebnisse, sondern oft sogar eine Verschlechterung.
Man sieht auch, daß der numerisch ermittelte Fehler ab ![]() plötzlich auf Null zurückgeht. Überlegen Sie sich die Ursache für
dieses Verhalten.
plötzlich auf Null zurückgeht. Überlegen Sie sich die Ursache für
dieses Verhalten.
Interessant ist das Verhalten des absoluten Fehlers für kleine Werte von
![]() : in diesem Bereich weicht die Fehlerabschätzung (6.20) stark
vom 'wahren' Fehler ab. Der Grund dafür liegt darin, daß in diesem
Bereich die Stützpunktdichte viel zu klein ist, um die (oszillierende)
Integrandenfunktion numerisch korrekt beschreiben zu können.
: in diesem Bereich weicht die Fehlerabschätzung (6.20) stark
vom 'wahren' Fehler ab. Der Grund dafür liegt darin, daß in diesem
Bereich die Stützpunktdichte viel zu klein ist, um die (oszillierende)
Integrandenfunktion numerisch korrekt beschreiben zu können.
Zusammenfassend kann jedoch gesagt werden, daß die Abschätzung des absoluten Fehlers im Romberg-Programm sehr gut funktioniert.
Viel problematischer ist die Fehlerdiagnostik für den relativen
Fehler, der an und für sich (s. Kapitel 1) viel mehr interessiert als der
absolute Fehler. Das Dilemma wird in den unteren Diagrammen der
Abbildungen 6.4 und 6.5 demonstriert:
Da für kleine und mittlere Werte ![]() des Romberg-Prozesses die
Integrationswerte noch sehr stark vom 'wahren' Integralwert abweichen,
kommt es für den relativen Fehler in diesem Bereich von
des Romberg-Prozesses die
Integrationswerte noch sehr stark vom 'wahren' Integralwert abweichen,
kommt es für den relativen Fehler in diesem Bereich von ![]() zu sehr
großen Unterschieden zwischen dem 'wahren' und dem geschätzten
relativen Fehler (s. speziell Abb. 6.5 (unten), wo Unterschiede
von bis zu 11(!) Zehnerpotenzen vorkommen). Das daraus resultierende
Fehlverhalten des Romberg-Programms wird im folgenden gezeigt:
zu sehr
großen Unterschieden zwischen dem 'wahren' und dem geschätzten
relativen Fehler (s. speziell Abb. 6.5 (unten), wo Unterschiede
von bis zu 11(!) Zehnerpotenzen vorkommen). Das daraus resultierende
Fehlverhalten des Romberg-Programms wird im folgenden gezeigt:
Angenommen, das Integral (6.21) soll auf eine relative
Genauigkeit von GEN=![]() berechnet werden. In diesem Fall
liefert das Romberg-Programm das folgende Ergebnis:
berechnet werden. In diesem Fall
liefert das Romberg-Programm das folgende Ergebnis:
NUM. METH. IN DER PHYSIK WS 2000/2001 ROMBERG-FORMEL 28-8-2000
INTEGRAL Skriptum (6.21) fuer n = 100
H. Sormann F90 DOUBLE PRECISION
m Funkt. num. Erg. wahrer geschaetzter relGEN
aufrufe rel. Fehler rel. Fehler
2 3 3.93611857 0.743152E+06 0.168200E+00 0.100000E-04
3 5 3.27406321 0.618154E+06 0.210069E-02 0.100000E-04
4 9 3.26718542 0.616855E+06 0.797950E-05 0.100000E-04
EXAKT = 0.0000052965
Ergebnis = 3.2671854208
geforderte Gen. (rel) = 0.100000E-04
Wahre Genauigkeit = 0.616855E+06
Dazu waren 9 Funktionsaufrufe noetig.
Auf Grund des Versagens der Fehlerdiagnose stoppt das Programm bereits bei
![]() ab und gibt ein Ergebnis, dessen relativer Fehler um mehr als 10
Zehnerpotenzen größer ist als GEN.
ab und gibt ein Ergebnis, dessen relativer Fehler um mehr als 10
Zehnerpotenzen größer ist als GEN.
Zumindest eine gewisse Möglichkeit, einem solchen Verhalten gegenzusteuern, bietet der im Abschnitt 6.6.1 angegebene Parameter KMIN. Dieser Wert gibt an, ab welcher Stufe des Romberg-Prozesses die Fehlerdiagnostik beginnen soll. Wenn man nun weiß, daß die Integrandenfunktion 'schwierig' ist (starke Oszillationen, Spitzen etc.), kann man durch die Eingabe eines geeignet großen Wertes von KMIN solche Probleme entschärfen.
Zum Beispiel gibt das Romberg-Programm für KMIN=6 das richtige Ergebnis:
NUM. METH. IN DER PHYSIK WS 2000/2001 ROMBERG-FORMEL 28-8-2000
INTEGRAL Skriptum (6.21) fuer n = 100
H. Sormann F90 DOUBLE PRECISION
(*) am Ende der Zeile bedeutet: keine Fehlerdiagnose.
m Funkt. num. Erg. wahrer geschaetzter relGEN
aufrufe rel. Fehler rel. Fehler
2 3 3.93611857 0.743152E+06 0.168200E+00 0.100000E-04 *
3 5 3.27406321 0.618154E+06 0.210069E-02 0.100000E-04 *
4 9 3.26718542 0.616855E+06 0.797950E-05 0.100000E-04 *
5 17 3.26715935 0.616850E+06 0.144805E+01 0.100000E-04 *
6 33 -1.46384560 0.276380E+06 0.107212E+01 0.100000E-04
7 65 0.10557102 0.199312E+05 0.984072E+00 0.100000E-04
8 129 0.00168158 0.316489E+03 0.180823E+01 0.100000E-04
9 257 -0.00135911 0.257604E+03 0.111862E+01 0.100000E-04
10 513 0.00016122 0.294385E+02 0.114146E+01 0.100000E-04
11 1025 -0.00002281 0.530572E+01 0.130154E+01 0.100000E-04
12 2049 0.00000688 0.298361E+00 0.232677E+00 0.100000E-04
13 4097 0.00000528 0.373724E-02 0.376226E-02 0.100000E-04
14 8193 0.00000530 0.109633E-04 0.109709E-04 0.100000E-04
15 16385 0.00000530 0.768462E-08 0.768636E-08 0.100000E-04
EXAKT = 0.0000052965
Ergebnis = 0.0000052965
geforderte Gen. (rel) = 0.100000E-04
berechnete Gen. (rel) = 0.768636E-08
Wahre Genauigkeit = 0.768462E-08
Dazu waren 16385 Funktionsaufrufe noetig.
Ausgangspunkt ist wieder die Gleichung (6.2), wobei vorläufig nur das
Integrationsintervall ![]() betrachtet wird:
betrachtet wird:
Man kann nun zeigen, daß die obige Gleichung erfüllt ist, wenn man für
![]() die Nullstellen des Legendre-Polynoms
die Nullstellen des Legendre-Polynoms ![]() -ter
Ordnung (
-ter
Ordnung (![]() ) verwendet.
Aus diesem Grund wird diese Quadraturformel auch als
Gauss-Legendre-Formel bezeichnet.
) verwendet.
Aus diesem Grund wird diese Quadraturformel auch als
Gauss-Legendre-Formel bezeichnet.
(o. B:) Die zugehörigen Gewichtsfaktoren ergeben sich aus
![\begin{displaymath}g_{j}=\frac{2}{(1-x_{j}^{2}) \left[ \frac{d}{dx} L_{m}(x) \right]
_{x=x_{j}}^{2}} . \end{displaymath}](img1063.gif)
Was die Verteilung der Stützpunkte im Intervall ![]() betrifft, so ist
diese natürlich nicht mehr äquidistant (s. Abb. 6.6), sondern hat
die folgenden Eigenschaften:
betrifft, so ist
diese natürlich nicht mehr äquidistant (s. Abb. 6.6), sondern hat
die folgenden Eigenschaften:
Bisher wurden alle Überlegungen zur Gauss-Quadratur für das spezielle
Intervall ![]() durchgeführt.
Die entsprechende Quadraturformel
durchgeführt.
Die entsprechende Quadraturformel
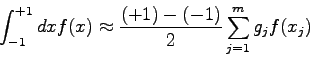
Wegen der Kompromisslosigkeit bei der Optimierung der Parameter ist zu
erwarten, daß die Gauss-Quadraturformel allen anderen Quadraturformeln
überlegen ist. Dies ist in vielen Fällen auch tatsächlich so: Betrachtet
man nämlich den Verfahrensfehler der Gauss-Quadratur (s. z.B. [16],
S.199)
Ein wichtiges Kriterium für die Anwendung der Gauss-Quadratur ist die
bequeme Verfügbarkeit der Gauss-Parameter ![]() und
und ![]() in
(6.23). Es gibt wohl keine ernstzunehmende Programm-Library, die nicht
über ein einschlägiges Generierungsprogramm verfügt. 'Numerical Recipes'
enthält die Routine GAULEG in FORTRAN ([9], S. 125f), PASCAL
([9], S. 700f) und C ([10], S. 152).
in
(6.23). Es gibt wohl keine ernstzunehmende Programm-Library, die nicht
über ein einschlägiges Generierungsprogramm verfügt. 'Numerical Recipes'
enthält die Routine GAULEG in FORTRAN ([9], S. 125f), PASCAL
([9], S. 700f) und C ([10], S. 152).
Die Routinen GAULEG.F90 bzw. GAULEG.C berechnen die Parameter der Gauss-Quadratur ('Gauss-Legendre-Parameter') für ein beliebiges Intervall und eine beliebige Ordnung:
INPUT-Parameter:
OUTPUT-Parameter:
Das Programm GAUINT berechnet näherungsweise ein bestimmtes Integral mittels der Gauss'schen Quadraturformel. Die erforderlichen Parameter werden von der Routine GAULEG (s. o.) berechnet.
INPUT-Parameter:
OUTPUT-Parameter:
Interne Parameter:
Struktogramm 19: Das Programm GAUINT.
=16cm
Struktogramm 19GAUINT(C,D,IREL,GEN,MANF,MINKR,MMAX,S,ERROR,
FEHLER)FEHLER:=TRUEMANF, MINKR ![]() 1print: 'GAUINT 'MANF oder MINKR
1print: 'GAUINT 'MANF oder MINKR ![]() 1'
1'
(return)......M:=MANF
OLDS:=1.E30GAULEG(C,D,Z,W,M)S:=0.0J=1(1)MS:=S+W(J)*FUNC(Z(J))ERROR:= ![]() S-OLDS
S-OLDS ![]() IREL = 1ERROR:=ERROR/
IREL = 1ERROR:=ERROR/ ![]() OLDS
OLDS ![]() ......ERROR
......ERROR ![]() GENFEHLER:=FALSE
GENFEHLER:=FALSE
S:=OLDS......OLDS:=S
M:=M+MINKRM ![]() MMAX .or. notFEHLER(return)
MMAX .or. notFEHLER(return)
Beim Romberg-Verfahren gibt es mit (6.20) eine Formel, die auf einfache
Weise eine in vielen Fällen zuverlässige Fehlerabschätzung ermöglicht.
Diese Methode ist auch im Programm GAUINT realisiert, d.h., man geht davon
aus, daß die Differenz zweier aufeinanderfolgender Näherungen der
Gauss-Quadratur (mit den Ordnungen M und M+MINKR) eine vernünftige
Abschätzung des absoluten Fehlers des Ergebnisses mit der Ordnung M
darstellt. Meine Tests haben gezeigt, daß diese Aussage (für nicht
zu große MINKR) ![]() unabhängig vom MINKR ist.
unabhängig vom MINKR ist.
![\includegraphics[scale=0.9]{num6_fig/aqua7}](img53.png) |
Im folgenden soll das Gauss-Legendre-Verfahren auf das 'schwierige'
Integral (6.21) für ![]() angewendet werden. Die Abb. 6.7
zeigt das
Verhalten des absoluten Fehlers in Abhängigkeit von der Ordnung der
Quadraturformel, d.h. von der Zahl der verwendeten Funktionswerte, wobei
wieder der 'wahre' Fehler dem numerisch geschätzten Fehler
gegenübergestellt ist.
angewendet werden. Die Abb. 6.7
zeigt das
Verhalten des absoluten Fehlers in Abhängigkeit von der Ordnung der
Quadraturformel, d.h. von der Zahl der verwendeten Funktionswerte, wobei
wieder der 'wahre' Fehler dem numerisch geschätzten Fehler
gegenübergestellt ist.
Die Ergebnisse sind im Prinzip ähnlich wie beim Romberg-Verfahren:
bis zu einer 'kritischen Ordnung' von etwa ![]() =320 ist der Verfahrensfehler
sehr groß; danach fällt er innerhalb eines relativ kleinen
Bereichs (
=320 ist der Verfahrensfehler
sehr groß; danach fällt er innerhalb eines relativ kleinen
Bereichs (![]() zwischen 320 und 370) auf den erreichbaren Mindestfehler
von ca.
zwischen 320 und 370) auf den erreichbaren Mindestfehler
von ca. ![]() ab. Zumindest in diesem Bereich ist die
Fehlerabschätzung gemäß Abschnitt 6.7.4 recht zuverlässig.
ab. Zumindest in diesem Bereich ist die
Fehlerabschätzung gemäß Abschnitt 6.7.4 recht zuverlässig.
Abb. 6.7 zeigt beeindruckend die große Leistungsfähigkeit
der Gauss-Quadratur gegenüber den anderen in diesem Kapitel behandelten
Methoden: selbst bei diesem sehr schwierig auszuwertenden Integral genügen
etwa 370 'Gauss-Stützpunkte', um eine Genauigkeit des Integrals
von ![]() zu erreichen! Beim Romberg-Verfahren ist dafür etwa
eine Ordnung 15 nötig (s. Abb. 6.5 oben), was weit mehr 10000
Stützpunkte bedeutet!
zu erreichen! Beim Romberg-Verfahren ist dafür etwa
eine Ordnung 15 nötig (s. Abb. 6.5 oben), was weit mehr 10000
Stützpunkte bedeutet!
Diese Überlegenheit der Gauss-Quadratur wird zwar auch im folgenden sehr deutlich, muß aber dennoch - wie sogleich demonstriert wird - kritisch betrachtet werden:
Für einen Vergleich der in diesem Kapitel präsentierten Verfahren soll als Qualitätskriterium die Rechenzeit herangezogen werden, die zur numerischen Berechnung eines bestimmten Integrals mit einer bestimmten Genauigkeit erforderlich ist. Da i.a. die zeitintensivste Komponente aller präsentierten Programme die Auswertung der Integrandenfunktion ist, kann man das Qualitätskriterium wie folgt definieren:
Jenes numerische Verfahren zur Berechnung bestimmter Integrale ist das beste, das zur Erlangung einer bestimmten Genauigkeit die kleinste Zahl von Stützpunkten benötigt.
Es soll nun als Test für die Trapezformel (Programm QTRAP),
das Romberg-Verfahren (Programm ROMB) und
die Gaussformel (Programm GAUINT) das bereits früher (s. S. 169)
verwendete bestimmte Integral
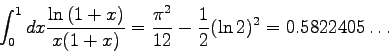
Definition: Ein uneigentliches Integral liegt vor, wenn
Selbstverständlich können die Probleme (1)-(3) auch in Kombination vorkommen!
Mathematische Formulierung:
Typ 1 (s. Abb. 6.9, links):
Typ 2 (s. Abb. 6.9, rechts):
Eine durchaus praktikable, wenn auch nicht sehr elegante Methode, mit
Integralen der Art
Diese einfache Methode ist jedoch nicht immer brauchbar. So müßte z.B.,
wenn man das uneigentliche Integral
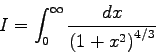
![\begin{displaymath}I = \int_{0}^{1} dt \frac{t^{2/3}}{\left[ t^{2}+(1-t)^{2} \right]^{4/3}} \end{displaymath}](img1088.gif)
.
2 Stuetzpunkte I = .103746E+01
6 Stuetzpunkte I = .111758E+01
12 Stuetzpunkte I = .112029E+01
20 Stuetzpunkte I = .112031E+01
30 Stuetzpunkte I = .112028E+01
42 Stuetzpunkte I = .112027E+01
56 Stuetzpunkte I = .112026E+01
72 Stuetzpunkte I = .112026E+01
90 Stuetzpunkte I = .112026E+01
110 Stuetzpunkte I = .112025E+01
132 Stuetzpunkte I = .112025E+01
Als Beispiel diene das uneigentliche Integral
Wie man allerdings der Abb. 6.10 entnehmen kann, muß man diese Ignoranz der Polstelle mit einer sehr schlechten Konvergenz des Verfahrens bezahlen!
Im Diagramm 6.10 ist dargestellt, wie das Gauss-Verfahren für die drei besprochenen Varianten konvergiert.
Integranden mit Unbestimmtheitsstellen an den Intervallgrenzen bereiten
offenen Quadraturformeln überhaupt keine Probleme. Verwendet man
geschlossene Quadraturformeln, muß man allerdings die
Unbestimmtheitsstellen explizite berücksichtigen. So würde z.B. das
Funktionsunterprogramm für den Integranden des Integrals
FUNCTION FUNC(x: real): real; BEGIN IF(x = 0.0)THEN func:=1.0 ELSE func:=sin(x)/x END;
Die soeben besprochene Gauss-Quadraturformel (6.22) ist nur
ein Spezialfall einer Gruppe von Quadraturformeln für die bestimmten
Integrale
Viele Libraries bieten Programme an, die die Stützpunkte und Gewichtsfaktoren einer ganzen Reihe solcher Sonderfälle berechnen (die Numerical Recipes C enthalten z. B. die Routinen GAULAG (Gauss-Laguerre), GAUHER (Gauss-Hermite) und andere); siehe dazu auch Abschnitt 6.11).
sind im Prinzip kein Problem. Wenn man sich auf Mehrfach-Integrale mit
konstanten Grenzen beschränkt, so gilt einfach
Für Integrale höherer Ordnung bzw. für Mehrfach-Integrale mit komplizierten Integranden sind statistische Methoden (Monte-Carlo-Methoden) von großer Bedeutung, insbesondere dann, wenn keine allzu hohe Genauigkeit gefordert wird!
SUBROUTINE D01BCF(ITYPE,A,B,C,D,N,WEIGHT,ABSCIS,IFAIL) INTEGER ITYPE,N,IFAIL REAL*8 A,B,C,D,WEIGHT(N),ABSCIS(N) . .
ITYPE=0 Gauss-Legendre
![]()
ITYPE=1 Gauss-Jacobi
![]()
ITYPE=2 Gauss-Exponential
![]()
ITYPE=3 Gauss-Laguerre
![]()
when ![]()
ITYPE=4 Gauss-Hermite
![]()
ITYPE=5 Gauss-Rational
![]()
when ![]() .
.
Die Ermittlung des Näherungswertes für das Integral lautet in allen
Fällen
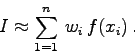
Ebenfalls in NAG: d01daf 2-D quadrature, finite region.
d01fbf Multi-dimensional Gauss.
d01gbf Multi-dimensional Monte Carlo.