Nächste Seite: Numerische Methoden zur Lösung Aufwärts: Numerische Methoden in der Vorherige Seite: Numerische Integration
Im Kapitel 2 standen lineare inhomogene Probleme der Art
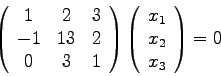
Es sind aber nicht Systeme vom Typus (7.1), um die es im folgenden
geht. Viel wichtiger für die praktische Anwendung sind nämlich homogene
Systeme der Art
Die Bedingungsgleichung für nicht-triviale Lösungen lautet demnach:
Ein sehr wichtiger Sonderfall des allgemeinen Eigenwertproblems (7.2)
ist das reguläre Eigenwertproblem mit
Für reguläre Eigenwertprobleme
Die Auswertung von (7.6) führt zu einem Polynom ![]() -ten Grades von
-ten Grades von
![]() , wenn
, wenn ![]() die Ordnung des linearen Systems (7.5) ist. Man
nennt dieses Polynom das charakteristische Polynom der Matrix
die Ordnung des linearen Systems (7.5) ist. Man
nennt dieses Polynom das charakteristische Polynom der Matrix ![]() :
:
Zu jedem Eigenwert ![]() gehört nun gemäß (7.5) ein
Eigenvektor
gehört nun gemäß (7.5) ein
Eigenvektor ![]() .
.
Wie bei den inhomogenen linearen Gleichungssystemen
spielt auch bei den Eigenwertproblemen die konkrete Form der Matrix ![]() eine wichtige Rolle. Im folgenden einige Fakten
zu diesem Thema:
eine wichtige Rolle. Im folgenden einige Fakten
zu diesem Thema:
Es gilt:
Alle Eigenwerte einer symmetrischen oder hermiteschen Matrix sind reell.
Eine sehr wichtige Frage ist es auch, ob eine Matrix diagonalisierbar
ist oder nicht.
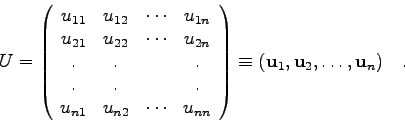
Diagonalisierbar heißt, daß eine nicht-singuläre Matrix ![]() existiert, welche die Matrix
existiert, welche die Matrix ![]() in eine Diagonalmatrix
in eine Diagonalmatrix ![]() überführt:
überführt:
Multipliziert man nämlich die Tranformationsvorschrift (7.8) von
links mit
![]() , so ergibt sich
, so ergibt sich
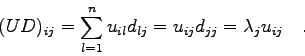
Die ![]() -te Spalte der Transformationsmatrix
-te Spalte der Transformationsmatrix ![]() stellt den
stellt den ![]() -ten
Eigenvektor der gegebenen Matrix
-ten
Eigenvektor der gegebenen Matrix ![]() dar.
dar.
Zusammenfassung: Wenn es gelingt, die Transformationsmatrix ![]() zu
finden, ist das vollständige Eigenwertproblem für die
Matrix
zu
finden, ist das vollständige Eigenwertproblem für die
Matrix ![]() gelöst!
gelöst!
Welche Matrizen sind diagonalisierbar?
Für normale Matrizen gilt also die wichtige Aussage:
Normale Matrizen können mittels orthogonaler bzw. unitärer
Transformationen auf Diagonalform gebracht werden:
Die numerische Behandlung von regulären Eigenwertproblemen stellt ein außerordentlich wichtiges und deshalb sehr gut entwickeltes Gebiet der Numerischen Mathematik dar. Typisch für dieses Gebiet ist die starke Spezialisierung der einzelnen Methoden. Der Benutzer muß also genau wissen, was er will, um das für sein Problem richtige Verfahren auszuwählen.
Einen kleinen Überblick über das vielfältige Software-Angebot bzgl. der Lösung von Eigenwertproblemen s. in Abschnitt 7.6.
Im folgenden soll versucht werden, Ihnen an Hand einiger einfacher und dennoch sehr effektiver numerischer Methoden die Grundideen der wichtigsten Verfahren klarzumachen. Eine auch nur annähernd vollständige Beschreibung der in der Literatur enthaltenen Methoden ist im Rahmen dieser LV. unmöglich und wird daher nicht angestrebt.
Im folgenden beschränken wir uns auf reelle Matrizen und beschreiben
Dieses iterative Verfahren liefert den betragsgrößten (bzw., wie später
gezeigt wird, auch den betragskleinsten) Eigenwert einer reellen Matrix ![]() .
.
Voraussetzung für die Anwendbarkeit dieses Verfahrens ist, daß die gegebene
Matrix diagonalisierbar ist (d.h., ein linear unabhängiges
Eigenvektorsystem hat), und daß ein betragsmäßig dominanter
Eigenwert existiert:
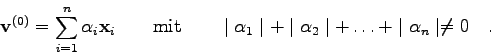
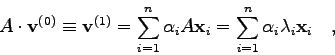
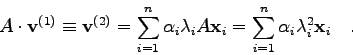
D.h.: Im Falle der Konvergenz strebt das Verhältnis der gleichen
Komponenten
aufeinanderfolgender Vektoren ![]() dem betragsgrößten
Eigenwert zu:
dem betragsgrößten
Eigenwert zu:
einer reellen Matrix ist für viele praktische Anwendungen von größerem Interesse als die Kenntnis des betragsgrößten Eigenwertes. Das Verfahren von v. Mises ist in der Lage, auch dieses Problem zu lösen.
Ausgehend von der Eigenwertgleichung (7.5)
Das heißt:
Nachdem aber die Kehrwerte der betragskleinsten Eigenwerte von ![]() natürlich die betragsgrößten Eigenwerte von
natürlich die betragsgrößten Eigenwerte von ![]() sind, braucht man
nur das v. Mises-Verfahren auf die Inverse der gegebenen Matrix anzuwenden,
um den betragskleinsten Eigenwert von
sind, braucht man
nur das v. Mises-Verfahren auf die Inverse der gegebenen Matrix anzuwenden,
um den betragskleinsten Eigenwert von ![]() zu erhalten.
zu erhalten.
Es gibt aber noch eine etwas andere Methode, die Mises-Iteration für den
betragskleinsten Eigenwert durchzuführen. Zu diesem Zweck braucht man nur
die Iterationsvorschrift für die Inverse von ![]() umzuformen:
umzuformen:
Auch ohne mathematische Beweisführung leuchtet ohne weiteres ein,
daß die Konvergenz der Iteration (7.22) umso besser sein wird,
je größer das Verhältnis
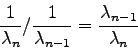
Angenommen, man kennt mit ![]() einen brauchbaren Schätzwert
für den betragskleinsten Eigenwert
einen brauchbaren Schätzwert
für den betragskleinsten Eigenwert ![]() . Nimmt man nun anstelle
der gegebenen Matrix
. Nimmt man nun anstelle
der gegebenen Matrix ![]() die Matrix
die Matrix
Die Überlegungen der Abschnitte 7.3.1 und 7.3.2 werden im folgenden Programm MISES realisiert.
Quelle: [2], S.94ff, Programm S.331f mit Änderungen.
Das Programm MISES berechnet den betragskleinsten Eigenwert und den zugehörigen Eigenvektor einer reellen Matrix (inklusive Spektralverschiebung).
INPUT-Parameter:
OUTPUT-Parameter:
INTERNE Parameter:
VERWENDETE PROZEDUREN:
Das Programm MISES braucht die Prozeduren NORM sowie die Prozeduren LUDCMP und LUBKSB (s. Kapitel 2).
=16cm
Struktogramm 21MISES(A,N,TMAX,GEN,V,EIGW0,EIGW,FEHLER) EPS:=1.0E-6
FEHLER:=TRUE
EIGALT:=0.0I=1(1)N A(I,I):=A(I,I) - EIGW0 LUDCMP(A,N,INDX,D,KHAD) T:=0 NORM(V,N) LUBKSB(A,N,INDX,V,W) SUM:=0.0
N1:=0 I=1(1)N ![]() W(I)
W(I)![]()
![]() EPS SUM:=SUM + V(I)/W(I)
EPS SUM:=SUM + V(I)/W(I)
N1:=N1 + 1......EIGW:=SUM/N1 EIGW:=EIGW + EIGW0![]() (EIGW-EIGALT)/EIGW
(EIGW-EIGALT)/EIGW![]()
![]() GEN FEHLER:=FALSEI=1(1)N V(I):=W(I) EIGALT:=EIGW T:=T+1 T
GEN FEHLER:=FALSEI=1(1)N V(I):=W(I) EIGALT:=EIGW T:=T+1 T ![]() TMAX .or. notFEHLER FEHLERprint 'MISES1 keine Konvergenz'NORM(V,N)(return)
TMAX .or. notFEHLER FEHLERprint 'MISES1 keine Konvergenz'NORM(V,N)(return)
Struktogramm 21a NORM(V,N) SUM:=0.0 I=1(1)N SUM:=SUM + V(I)*V(I) SUM:=SQRT(SUM) SUM ![]() 0.0 I=1(1)N V(I):=V(I)/SUMprint 'NORM Nullvektor'(return)
0.0 I=1(1)N V(I):=V(I)/SUMprint 'NORM Nullvektor'(return)
Die folgenden Test-Beispiele sollen dazu dienen, die Zuverlässigkeit des Programms MISES zu überprüfen.
Die Tests beginnen mit der 4x4-Matrix
3.8000 1.8000 -2.0000 -0.6000
5.4000 6.2000 -7.2000 -1.0000
2.0000 2.4000 -2.0000 0.0000
1.8000 1.0000 0.0000 1.0000
Es soll der betragskleinste Eigenwert bzw. der zugehörige Eigenvektor berechnet werden.
Das exakte Ergebnis lautet
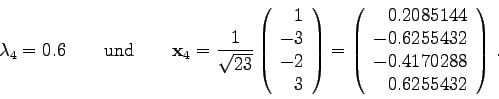
.
MISES-Test: n = 4 rel. Gen. = 1.0000000000E-06
Schaetzwert fuer EW = 0.000000
Matrix und Anfangsvektor:
3.8000 1.8000 -2.0000 -0.6000 1.0000
5.4000 6.2000 -7.2000 -1.0000 1.0000
2.0000 2.4000 -2.0000 0.0000 1.0000
1.8000 1.0000 0.0000 1.0000 1.0000
betragskleinster Eigenwert nach 20 Iterationen = 0.600000
Eigenvektor:
1 -0.208514
2 0.625543
3 0.417029
4 -0.625543
Nimmt man als Schätzwert
![]() , so liefert das Programm
MISES1:
, so liefert das Programm
MISES1:
.
MISES-Test: n = 4 rel. Gen. = 1.0000000000E-06
Schaetzwert fuer EW = 0.500000
Matrix und Anfangsvektor:
3.8000 1.8000 -2.0000 -0.6000 1.0000
5.4000 6.2000 -7.2000 -1.0000 1.0000
2.0000 2.4000 -2.0000 0.0000 1.0000
1.8000 1.0000 0.0000 1.0000 1.0000
betragskleinster Eigenwert nach 8 Iterationen = 0.600000
Eigenvektor:
1 -0.208514
2 0.625543
3 0.417029
4 -0.625543
Anmerkung:
Wie Sie sehen, gibt MISES1 nicht den theoretisch vorgegebenen Eigenvektor,
sondern diesen Vektor mal dem Faktor (-1). Liegt hier ein
Fehlverhalten des Programmes vor?
Zuletzt noch ein MISES1-Test für die 3x3-Matrix
1.0000 0.0000 -1.0000
1.0000 2.0000 1.0000
-2.0000 -2.0000 2.0000
mit den entarteten Eigenwerten 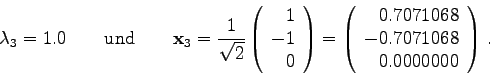
.
MISES-Test: n = 3 rel. Gen. = 1.0000000000E-06
Schaetzwert fuer EW = 0.000000
Matrix und Anfangsvektor:
1.0000 0.0000 -1.0000 1.0000
1.0000 2.0000 1.0000 0.0000
-2.0000 -2.0000 2.0000 0.0000
betragskleinster Eigenwert nach 24 Iterationen = 1.000000
Eigenvektor:
1 0.707107
2 -0.707107
3 0.000000
Dieses
Verfahren ist geeignet, das vollständige Eigenwertproblem symmetrischer
Matrizen zu lösen.
Gegeben ist also eine reelle Matrix
Das Prinzip des Jacobi-Verfahrens besteht aus einer orthogonalen
Transformation der Matrix ![]() in eine Diagonalmatrix
in eine Diagonalmatrix ![]() (vgl. Kap. 7.1.1):
(vgl. Kap. 7.1.1):
Das Problem besteht nun darin, die Transformationsmatrix ![]() zu ermitteln.
Beim Jacobi-Verfahren wird die Transformation (7.24) durch eine
sukzessive Folge von Ähnlichkeitsoperationen ersetzt.
Selbstverständlich müssen auch die dabei verwendeten
Transformationsmatrizen
zu ermitteln.
Beim Jacobi-Verfahren wird die Transformation (7.24) durch eine
sukzessive Folge von Ähnlichkeitsoperationen ersetzt.
Selbstverständlich müssen auch die dabei verwendeten
Transformationsmatrizen
![]() orthogonal sein.
orthogonal sein.
Anstelle von (7.24) gilt also:
Die beim Jacobi-Verfahren verwendeten Matrizen ![]() haben die allgemeine
Form einer orthogonalen Drehmatrix
haben die allgemeine
Form einer orthogonalen Drehmatrix
![\includegraphics[scale=0.9]{num7_fig/ortho}](img57.png)
Wie man sofort sieht, ist ![]() durch drei Angaben eindeutig
bestimmt:
durch drei Angaben eindeutig
bestimmt:
![]() und
und ![]() geben jene Zeilen bzw. Spalten der Matrix an, an deren
Schnittpunkten sich die Drehmatrix von einer Einheitsmatrix unterscheidet.
geben jene Zeilen bzw. Spalten der Matrix an, an deren
Schnittpunkten sich die Drehmatrix von einer Einheitsmatrix unterscheidet.
![]() ist der Drehwinkel. Es kann leicht gezeigt werden, daß
ist der Drehwinkel. Es kann leicht gezeigt werden, daß
![]() - unabhängig von den Argumenten - stets orthogonal
ist, d.h. daß
gilt:
- unabhängig von den Argumenten - stets orthogonal
ist, d.h. daß
gilt:
Bevor nun über die optimale Wahl der Parameter ![]() für jeden
Iterationsschritt gesprochen wird, soll im Detail untersucht werden, was bei
einer Transformation
für jeden
Iterationsschritt gesprochen wird, soll im Detail untersucht werden, was bei
einer Transformation
Als nächstes soll (7.27) unter der Bedingung ausgewertet werden,
daß ![]() und
und ![]() weder
weder ![]() noch
noch ![]() sind. Unter diesen Umständen sind
die Komponenten der Drehmatrix (7.25) einfach 'Kronecker-Deltas',
und man erhält
sind. Unter diesen Umständen sind
die Komponenten der Drehmatrix (7.25) einfach 'Kronecker-Deltas',
und man erhält
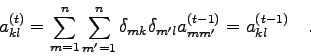
Das bedeutet: Bei der Transformation bleiben alle Komponenten von ![]() ,
die weder den Index
,
die weder den Index ![]() noch den Index
noch den Index ![]() enthalten, unverändert.
enthalten, unverändert.
Die noch fehlenden Komponenten aus der ![]() -ten und
-ten und ![]() -ten Zeile und Spalte
können ebenfalls unter Verwendung von (7.27) bestimmt werden:
-ten Zeile und Spalte
können ebenfalls unter Verwendung von (7.27) bestimmt werden:
Nun fehlen nur noch die Komponenten
Der Zweck jeder der orthogonalen Transformationen, der die Matrix ![]() unterzogen wird, ist der, die entstehenden Matrizen
unterzogen wird, ist der, die entstehenden Matrizen
Ein Maß dafür, inwieweit dies gelungen ist,
ist offenbar die Summe ![]() der Quadrate der Nicht-Diagonalelemente der Matrix:
der Quadrate der Nicht-Diagonalelemente der Matrix:
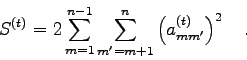
Ohne Beweis: Es läßt sich zeigen, daß die Differenz von
![]() und
und ![]() einfach dem Ausdruck
einfach dem Ausdruck
Die Gleichung (7.33) führt zur sinnvollsten Strategie bei der
Auswahl der noch offenen Parameter ![]() ,
, ![]() und
und ![]() für einen
bestimmten Iterationsschritt:
für einen
bestimmten Iterationsschritt:
Die Verkleinerung von ![]() ist dann ein Maximum,
ist dann ein Maximum,
Wählt man nun vor jedem Iterationsschritt die Parameter der Drehmatrix
(7.25) auf die soeben beschriebene Weise, ist eine monotone
Abnahme von ![]()
Zusätzlich soll auch noch jene Matrix berechnet werden, die sich aus dem
Produkt der einzelnen Transformationsmatrizen ergibt:
Das Programm JACOBI löst das vollständige Eigenwertproblem einer reellen, symmetrischen Matrix.
INPUT-Parameter:
OUTPUT-Parameter:
=16cm
Struktogramm 22JACOBI(A,N,TMAX,EIGVEK)PI=3.14159265
EPS:=1.e-8I=1(1)NJ=1(1)NI = JEIGVEK(I,I):=1.0EIGVEK(I,J):=0.0
Struktogramm 23(Fortsetzung)T:=0T:=T+1SUMME:=0.0I=1(1)N-1J=I+1(1)NSUMME:=SUMME+2.0*A(I,J)*A(I,J)IF(SUMME=0.0) ===![]() (return)GRENZE:=SQRT(SUMME)/N/NI=1(1)N-1J=I+1(1)N
(return)GRENZE:=SQRT(SUMME)/N/NI=1(1)N-1J=I+1(1)N![]() A(I,J)
A(I,J) ![]()
![]() GRENZENENNER:=A(I,I)-A(J,J)
GRENZENENNER:=A(I,I)-A(J,J)![]() NENNER/A(I,J)
NENNER/A(I,J) ![]()
![]() EPSPHI:=PI/4.0PHI:=0.5*ATAN(2.0*A(I,J)
EPSPHI:=PI/4.0PHI:=0.5*ATAN(2.0*A(I,J)
/NENNER)SINUS:=SIN(PHI)
COSIN:=COS(PHI)K=I+1(1)J-1SPEICH:=A(I,K)
A(I,K):=COSIN*A(I,K)+SINUS*A(K,J)
A(K,J):=COSIN*A(K,J)-SINUS*SPEICHK=J+1(1)NSPEICH:=A(I,K)
A(I,K):=COSIN*A(I,K)+SINUS*A(J,K)
A(J,K):=COSIN*A(J,K)-SINUS*SPEICHK=1(1)I-1SPEICH:=A(K,I)
A(K,I):=COSIN*A(K,I)+SINUS*A(K,J)
A(K,J):=COSIN*A(K,J)-SINUS*SPEICHSPEICH:=A(I,I)
A(I,I):=COSIN**2*A(I,I)+2.0*COSIN*SINUS*A(I,J)+SINUS**2*A(J,J)
A(J,J):=COSIN**2*A(J,J)-2.0*COSIN*SINUS*A(I,J)+SINUS**2*SPEICH
A(I,J):=0.0K=1(1)NSPEICH:=EIGVEK(K,J)
EIGVEK(K,J):=COSIN*EIGVEK(K,J)-SINUS*EIGVEK(K,I)
EIGVEK(K,I):=COSIN*EIGVEK(K,I)+SINUS*SPEICH......T ![]() TMAXprint 'JACOBI Konvergenz nicht erreicht'
TMAXprint 'JACOBI Konvergenz nicht erreicht'
(return)
Programm-Struktur:
Die Konvergenz des Jacobi-Verfahrens ist zumeist so gut, daß man die Rechnung bis zum 'Underflow' von SUMME treiben kann. Die obige Abfrage auf die exakte Null funktioniert jedoch nur dann, wenn vom System her ein Underflow als Null interpretiert wird!
Wenn SUMME=0.0, Return ins aufrufende Programm.
Wenn SUMME![]() 0.0, werden Matrix-Transformationen gemäß
(7.28 - 7.32) bzgl. all jener
Nicht-Diagonalelemente durchgeführt, deren Beträge
0.0, werden Matrix-Transformationen gemäß
(7.28 - 7.32) bzgl. all jener
Nicht-Diagonalelemente durchgeführt, deren Beträge ![]() GRENZE sind.
GRENZE sind.
In FORTRAN-, PASCAL-, ... -Programmen kann die Berechnung des idealen
Drehwinkels gemäß Glg. (7.34) erfolgen.
In Programmiersprachen ohne Arcustangens-Funktion wie z. B. in C kann die
Berechnung von ![]() und
und ![]() auf die folgende Weise
geschehen (mathematische Darstellung s. [10], S. 464f):
auf die folgende Weise
geschehen (mathematische Darstellung s. [10], S. 464f):
.
g=100*fabs(a[i][j]);
if(fabs(a[i][j]) > grenze) {
h=a[i][i]-a[j][j];
// This if statement prevents an overflow of theta*theta in the following
// statement.
if(fabs(h)+g == fabs(h)) tfac=a[i][j]/h;
else {
theta=h/2.0/a[i][j];
tfac=1.0/(fabs(theta)+sqrt(1.0+theta*theta));
if(theta<0.0)tfac=-tfac;
}
cosin=1.0/sqrt(tfac*tfac+1.0);
sinus=tfac*cosin;
.
Matrix: 5.000 4.000 1.000 1.000
4.000 5.000 1.000 1.000
1.000 1.000 4.000 2.000
1.000 1.000 2.000 4.000
exakte Loesung:
Eigenwert: Eigenvektor:
10 (2,2,1,1)/sqrt(10) = (0.6324555, 0.6324555, 0.3162278, 0.3162278)
1 (-1,1,0,0)/sqrt(2) = (-0.7071068, 0.7071068, 0.0, 0.0)
5 (-1,-1,2,2)/sqrt(10) = (-0.3162278, -0.3162278, 0.6324555, 0.6324555)
2 (0,0,-1,1)/sqrt(2) = (0.0, 0.0, -0.7071068, 0.7071068)
Jacobi-Loesung:
Eigenwert: Eigenvektor:
10.000000 0.632456 0.632456 0.316228 0.316228
1.000000 -0.707107 0.707107 -0.000000 -0.000000
5.000000 -0.316228 -0.316228 0.632456 0.632456
2.000000 -0.000000 -0.000000 -0.707107 0.707107
.
Matrix: 6.000 4.000 4.000 1.000
4.000 6.000 1.000 4.000
4.000 1.000 6.000 4.000
1.000 4.000 4.000 6.000
exakte Loesung:
Eigenwert: Eigenvektor:
15 0.5 0.5 0.5 0.5
-1 0.5 -0.5 -0.5 0.5
5 -0.5 0.5 -0.5 0.5
5 -0.5 -0.5 0.5 0.5
Jacobi-Loesung:
Eigenwert: Eigenvektor:
15.000000 0.500000 0.500000 0.500000 0.500000
-1.000000 -0.500000 0.500000 0.500000 -0.500000
5.000000 0.226248 -0.669934 0.669934 -0.226248
5.000000 -0.669934 -0.226248 0.226248 0.669934
Zu diesen Ergebnissen noch zwei Anmerkungen:
Gegeben ist ein System von ![]() gekoppelten Federpendeln, wobei die
schwingenden Körper die Massen
gekoppelten Federpendeln, wobei die
schwingenden Körper die Massen ![]() ,
, ![]() haben:
haben:
![\includegraphics[scale=0.8]{num7_fig/oszill1}](img58.png)
Für die weitere Diskussion werden die folgenden Annahmen gemacht:
Die momentanen Auslenkungen der Massenpunkte
werden mit ![]() bezeichnet,
und die Kräfte zwischen den Massen werden im Sinne einer harmonischen
Näherung als proportional zu ihren
Abständen angenommen. Der Proportionalitätsfaktor
zwischen Abstand und Kraft, die Federkonstante
bezeichnet,
und die Kräfte zwischen den Massen werden im Sinne einer harmonischen
Näherung als proportional zu ihren
Abständen angenommen. Der Proportionalitätsfaktor
zwischen Abstand und Kraft, die Federkonstante ![]() ,
wird in cgs-Einheiten (dyn/cm) angegeben.
,
wird in cgs-Einheiten (dyn/cm) angegeben. ![]() ist der Abstand zwischen 2
Massepunkten in der Ruhelage:
ist der Abstand zwischen 2
Massepunkten in der Ruhelage:
![\includegraphics[scale=0.8]{num7_fig/oszill2}](img59.png)
Wird ein solches System in Schwingungen versetzt und dann sich selbst
überlassen, so läßt sich für jeden Massenpunkt eine
Bewegungsgleichung der Art
Beschränkt man sich bei der Lösung dieses Systems auf kleine Auslenkungen,
so kann das System (7.38)
unter Verwendung der Ansatzfunktion
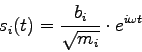
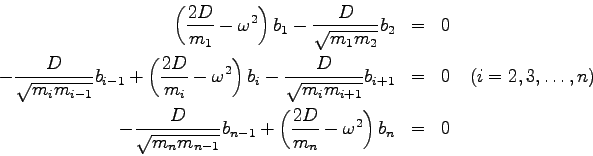
![\includegraphics[scale=0.8]{num7_fig/oszill3}](img60.png)
wobei
![]() gesetzt wurde. Die (reellen) Eigenwerte der obigen
symmetrisch-tridiagonalen Matrix sind also die Quadrate der Eigenfrequenzen des schwingenden Systems (kleinste Frequenz=Grundschwingung
und
gesetzt wurde. Die (reellen) Eigenwerte der obigen
symmetrisch-tridiagonalen Matrix sind also die Quadrate der Eigenfrequenzen des schwingenden Systems (kleinste Frequenz=Grundschwingung
und ![]() Oberschwingungen).
Oberschwingungen).
Testbeispiel "Federpendel" fuer Jacobi: ======================================= Federkonstante [dyn/cm] = 25.000 5 Massenpunkte: m1 = 3 g m2 = 6 g m3 = 9 g m4 = 2 g m5 = 6 g JACOBI liefert das folgende Resultat: nr lambda(1/s/s) Kreisfrequenz(1/s) 1 19.858498 4.456287 2 1.135214 1.065464 (Grundschwingung) 3 5.525477 2.350633 4 29.036367 5.388540 5 8.333333 2.886751
Viele interessante physikalisch-technische Problemstellungen führen nicht
unmittelbar zu einem Eigenwertproblem vom Typus (7.5), sondern auf ein
homogenes lineares Gleichungssystem in der Art
Wie kann man nun das erweiterte Eigenwertproblem (7.40) auf die
Form
Leider ist diese simple Umformung nicht sehr brauchbar, weil nämlich die neue
Koeffizentenmatrix ![]() die wichtige Eigenschaft der Symmetrie verloren hat:
die wichtige Eigenschaft der Symmetrie verloren hat:
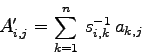
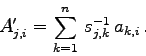
Eine bessere, allerdings etwas aufwändigere Methode der Umformung soll nun präsentiert werden:
Ausgangspunkt ist die sogenannte Cholesky decomposition der symmetrischen,
positiv-definiten Matrix ![]() :
:
Hat man die Cholesky-Prozedur erledigt, ist die weitere Vorgangsweise relativ
einfach: Einsetzen von Glg. (7.41) in die erweiterte Eigenwertgleichung
(7.40) gibt
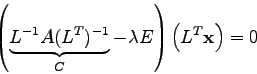
Aus den Eigenvektoren ![]() des Systems (7.42) können mittels
des Systems (7.42) können mittels
Die Formeln, die zur numerischen Ausführung der Cholesky decomposition
erforderlich sind, können ohne Schwierigkeiten hergeleitet werden. Man geht dabei
von der Komponentendarstellung von Glg. (7.41) aus:
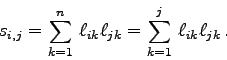
Für die erste Spalte (![]() ) erhält man sofort
) erhält man sofort
Analog erhält man für die zweite Spalte (![]() )
)
Aus diesen Gleichungen kann man ohne weiteres auf die allgemeinen Cholesky-Formeln
schließen:
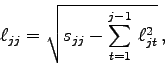
Zu diesem Gleichungen noch 2 Anmerkungen:
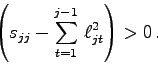
Die numerische Auswertung der Gleichungen (7.44) wird im folgenden Struktrogramm
Nr. 23 CHOLESKY beschrieben. Um genau zu sein, im ersten (kleineren) Teil dieses
Programms. Der zweite Teil von CHOLESKY beschreibt die numerische Auswertung der neuen
Matrix ![]() gemäß Glg. (7.42). Den entsprechenden Algorithmus-Teil im
Struktogramm 23 habe ich dem Algol-Programm reduc1 von Martin und
Wilkinson7.5 entnommen.
Ich muß gestehen, daß ich bisher noch keine Zeit
fand, diesen Algorithmus schlüssig aus der Gleichung (7.42) nachzuvollziehen.
gemäß Glg. (7.42). Den entsprechenden Algorithmus-Teil im
Struktogramm 23 habe ich dem Algol-Programm reduc1 von Martin und
Wilkinson7.5 entnommen.
Ich muß gestehen, daß ich bisher noch keine Zeit
fand, diesen Algorithmus schlüssig aus der Gleichung (7.42) nachzuvollziehen.
INPUT-Parameter:
OUTPUT-Parameter:
=16cm
Struktogramm 23CHOLESKY(N,A,S,FEHLER)FEHLER:=0I=1(1)NJ=I(1)NX:=S(I,J)K=1(1)I-1X:=X-S(I,K)*S(J,K)J ![]() IS(J,I):=X/YX
IS(J,I):=X/YX ![]() 0.0FEHLER:=1
0.0FEHLER:=1
print 'Matrix S nicht pos-def.'
(return)......Y:=SQRT(X)
S(I,I):=YAnmerkung: Ende der Cholesky Decomposition.Anmerkung: Nun beginnt die Berechnung der Matrix C (Achtung: Abspeicherung auf A):I=1(1)NY:=B(I,I)J=I(1)NX:=A(I,J)K=1(1)I-1X:=X-S(I,K)*A(J,K)A(J,I):=X/YJ=1(1)NI=J(1)NX:=A(I,J)K=J(1)I-1X:=X-A(K,J)*S(I,K)K=1(1)J-1X:=X-A(J,K)*S(I,K)A(I,J):=X/S(I,I)I=1(1)N-1J=I+1(1)NA(I,J):=A(J,I)
S(I,J):=0.0
TESTBEISPIEL:
=============
Numerische Loesung des erweiterten Eigenwertproblems
[A - lambda . B] x = 0
Matrix A (symmetrisch):
5.0000 4.0000 1.0000 1.0000
4.0000 5.0000 1.0000 1.0000
1.0000 1.0000 4.0000 2.0000
1.0000 1.0000 2.0000 4.0000
Matrix B (symmetrisch und positiv-definit):
5.0000 7.0000 6.0000 5.0000
7.0000 10.0000 8.0000 7.0000
6.0000 8.0000 10.0000 9.0000
5.0000 7.0000 9.0000 10.0000
Das Programm CHOLESKY gewinnt aus den gegebenen Matrizen
A und B mittels Cholesky-Aufspaltung von B:
B = L . L^T
die Matrix
C = L^(-1) . A . (L^(-1))^T
Die untere Dreiecksmatrix L lautet:
2.2361 0.0000 0.0000 0.0000
3.1305 0.4472 0.0000 0.0000
2.6833 -0.8944 1.4142 0.0000
2.2361 -0.0000 2.1213 0.7071
Diese Matrix C ist symmetrisch und hat dasselbe
Eigenwertspektrum wie das gegebene erweiterte Eigenwertproblem:
1.0000 -3.0000 -3.4785 7.9057
-3.0000 18.0000 16.4438 -41.1096
-3.4785 16.4438 18.0000 -43.0000
7.9057 -41.1096 -43.0000 110.0000
Mit dem Jacobi-Programm koennen die 4 Eigenwerte der
Matrix C ohne weiteres bestimmt werden.
Die Eigenwerte lauten: 0.2623 2.3078 1.1530 143.2769
Das Jacobi-Verfahren ist im Prinzip für alle reellen symmetrischen Matrizen
ausgezeichnet geeignet. Dennoch bieten die meisten 'Profi-Bibliotheken'
noch weitere leistungsfähige Programme an, die für Matrizen höherer
Ordnung (![]() 20) deutlich schneller sind als das Jacobi-Verfahren7.6.
20) deutlich schneller sind als das Jacobi-Verfahren7.6.
Die Grundidee dieser Programme ist ein Zwei-Stufen-Prozess:
Sowohl die Householder- als auch die QR- (QL-)Methode kann im Rahmen dieser Lehrveranstaltung nicht im Detail erörtert werden. Eine sehr gute und kompakte Darstellung der Theorie sowie die entsprechenden Programme TRED2 (Householder) und TQLI (QL-Algorithmus) finden Sie in [9] und in [10].
Genauere Informationen über diese modernen Methoden erhalten Sie auch in meiner weiterführenden Lehrveranstaltung
Dieses Problem wird in der Numerik i. a. ähnlich angegangen wie bei den
symmetrischen Matrizen, nämlich mittels eines zweistufigen Prozesses.
Dabei wird (1) die Matrix ![]() durch einen nicht-iterativen
Algorithmus in eine einfachere Form gebracht (s. u.), und (2) werden die
Eigenwerte der so erhaltenen Matrix bestimmt.
durch einen nicht-iterativen
Algorithmus in eine einfachere Form gebracht (s. u.), und (2) werden die
Eigenwerte der so erhaltenen Matrix bestimmt.
Die Grundidee basiert auf den folgenden Aussagen aus der
Matrizentheorie:
Jede Matrix kann durch einen nicht-iterativen
Ähnlichkeits-Prozess auf eine Upper Hessenberg Form (UHF) gebracht
werden.
und
Bei einer Upper-Hessenberg-Matrix sind alle Matrix-Komponenten unterhalb der ersten unteren Nebendiagonale Null.
Die Umformung einer allgemeinen reellen Matrix auf eine UHF geschieht mit einem Algorithmus, der dem Gauss'schen Eliminationsverfahren (s. Kap. 2, LU-Decomposition) ähnlich ist, nur mit dem wichtigen Unterschied, daß im gegebenen Fall jede Umwandlung der Matrix eine Ähnlichkeitsoperation sein muß. Im folgenden soll dieser Algorithmus kurz erläutert werden:
Angenommen, eine 7x7-Matrix soll in die UHF gebracht werden, und der Algorithmus habe bereits einen Teil der Arbeit erledigt d.h. er habe (z. B.) bereits die ersten drei Spalten der Matrix auf Upper-Hessenberg gebracht. Dann sieht die Matrix so aus:
x x x x x x x
x x x x x x x
0 x x x x x x
0 0 x x x x x
0 0 0 a x x x
0 0 0 b x x x
0 0 0 c x x x
Im nun folgenden Schritt soll die vierte Spalte auf UHF gebracht werden,
d.h. die letzten beiden Werte dieser Spalte sollen Null werden.
Dies erreicht man dadurch, daß man die drittletzte Zeile der Matrix
mit den Faktoren (b/a) bzw. (c/a) multipliziert und diese zur vorletzten
bzw. letzten Zeile addiert.
Wie Sie sich erinnern (Kap. 2, LU-Decomposition),
ist es bei solchen Rechnungen wichtig, darauf zu achten, daß die
Multiplikatoren dem Betrage nach so klein als möglich gehalten werden:
dies erreicht man durch Pivotisierung, d.h. dadurch, daß man
die in Diskussion stehenden Zeilen (im konkreten Fall diejenigen, welche
a, b und c enthalten) so vertauscht, daß an der Stelle 'a' die
betragsgrößte der Zahlen a, b, c zu stehen kommt.
In einem wichtigen Punkt unterscheidet sich das hier zu diskutierende
Verfahren von der LU-Decomposition: um zu gewährleisten, daß
die Umformung der gegebenen Matrix ![]() in eine UHF eine
Ähnlichkeitsoperation ist, müssen alle Zeilenvertauschungen bei der
Pivotisierung und alle Zeilenadditionen zur Erreichung der
'Hessenberg-Nullen' durch analoge Operationen bzgl. der Spalten ergänzt
werden.
in eine UHF eine
Ähnlichkeitsoperation ist, müssen alle Zeilenvertauschungen bei der
Pivotisierung und alle Zeilenadditionen zur Erreichung der
'Hessenberg-Nullen' durch analoge Operationen bzgl. der Spalten ergänzt
werden.
Das Programm ELMHES reduziert eine allgemeine reelle Matrix in die entsprechende 'Upper-Hessenberg-Matrix'.
Quelle: [9], S. 752; [10], S. 485f.
INPUT-Parameter:
OUTPUT-Parameter:
=16cm
Struktogramm 24ELMHES(A,N,FEHLER)N ![]() 3FEHLER:=TRUE
3FEHLER:=TRUE
print 'ELMHES Ordnung
der Matrix ![]() 3' FEHLER:=FALSE M=2(1)N-1 X:=0.0
3' FEHLER:=FALSE M=2(1)N-1 X:=0.0
I:=M J=M(1)N![]() A(J,M-1)
A(J,M-1)![]()
![]()
![]() X
X ![]() X:=A(J,M-1)
X:=A(J,M-1)
I:=J...... I ![]() M J=M-1(1)N Y:=A(I,J)
M J=M-1(1)N Y:=A(I,J)
A(I,J):=A(M,J)
A(M,J):=Y J=1(1)N Y:=A(J,I)
A(J,I):=A(J,M)
A(J,M):=Y...... X ![]() 0.0 I=M+1(1)N Y:=A(I,M-1) Y
0.0 I=M+1(1)N Y:=A(I,M-1) Y ![]() 0.0 Y:=Y/X
0.0 Y:=Y/X
A(I,M-1):=Y J=M(1)N A(I,J):=A(I,J) - Y*A(M,J) J=1(1)N A(J,M):=A(J,M) - Y*A(J,I)............(return)
Um die reellen und konjugiert-komplexen Eigenwerte einer reellen
Upper-Hessenberg-Matrix zu berechnen, kann wieder der bereits im Abschnitt
7.4.9 erwähnte QR-Algorithmus zum Einsatz kommen. Ein Beispiel für ein
derartiges Programm finden Sie in den Numerical Recipes (Theorie und
FORTRAN-Programm in [9], S. 374f; PASCAL-Programm in [9],
S. 753f; Theorie und C-Programm in [10], S. 486ff.
Weitere einschlägige Programme siehe auch im Abschnitt 7.6.
Auch über den QR-Algorithmus können Sie in meiner weiterführenden Lehrveranstaltung
Wenn man sich mit den reellen Eigenwerten und Eigenvektoren einer Matrix in UHF begnügt, gibt es auch eine viel einfachere Methode als QR; diese soll im folgenden beschrieben werden:
Wie Sie dem Abschnitt 7.1 entnehmen können, sind die Eigenwerte einer
Matrix zugleich die Nullstellen ihres charakteristischen Polynoms
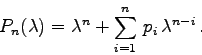
Man kann jedoch im Falle einer Upper-Hessenberg-Matrix das charakteristische Polynom auswerten, ohne explizite dessen Koeffizienten zu kennen; dies wird im folgenden Abschnitt erläutert.
Hyman konnte zeigen, daß für Hessenberg-Matrizen das
Polynom
![]() die Form
die Form
Eine einfache Rechnung zeigt nun, daß die ![]() unbekannten Koeffizienten
des Vektors
unbekannten Koeffizienten
des Vektors ![]() mittels
mittels
INPUT-PARAMETER:
=12cm Struktogramm 25FUNCTION HYMAN(UHM,N,LAM) X(N):=1.0 I=N-1(-1)1 SUM:= LAM*X(I+1) L=0(1)N-I-1 SUM:=SUM - UHM(I+1,N-L)*X(N-L) X(I):= SUM/UHM(I+1,I) SUM:=-LAM*X(1) I=1(1)N SUM:=SUM + UHM(1,I)*X(I) HYMAN:=SUM(return)
Wenn man die gegebene Matrix mittels ELMHES auf die UHF bringt,
und diese Matrix als Input von HYMAN nimmt, so erhält man schnell und
genau die Funktionswerte von ![]() . Die Nullstellen dieser Kurve
sind bekanntlich die (reellen) Eigenwerte der gegebenen Matrix. Um diese
Nullstellen numerisch zu ermitteln, müssen also die Programme ELMHES,
HYMAN und (z. B.) INTSCH geeignet kombiniert werden.
. Die Nullstellen dieser Kurve
sind bekanntlich die (reellen) Eigenwerte der gegebenen Matrix. Um diese
Nullstellen numerisch zu ermitteln, müssen also die Programme ELMHES,
HYMAN und (z. B.) INTSCH geeignet kombiniert werden.
Die Abb. 7.2 zeigt die Funktion ![]() für die 4x4-Matrix von
Seite 207. Die vier Eigenwerte lauten: 0.6, 1.2, 2.4 und 4.8.
für die 4x4-Matrix von
Seite 207. Die vier Eigenwerte lauten: 0.6, 1.2, 2.4 und 4.8.
Die Hyman'sche Methode kann besonders einfach auf tridiagonale Matrizen der Form
![\includegraphics[scale=0.9]{num7_fig/ahess3}](img63.png)
angewendet werden, also auf Matrizen, die durch die drei Diagonalvektoren
![]() ,
, ![]() und
und ![]() bestimmt werden. Man erhält durch
Spezialisierung von (7.46) und (7.47) die Formeln
bestimmt werden. Man erhält durch
Spezialisierung von (7.46) und (7.47) die Formeln
Es folgt nun ein Programmiervorschlag (in C) für die numerische Bestimmung der reellen Eigenwerte allgemeiner reeller tridiagonaler Matrizen:
.
#include <stdio.h>
#include <math.h>
#include "nrutil.c"
int n;
double *a,*b,*c;
double hymtri(double lam)
// Diese Routine dient zur Auswertung der 'Hyman-Funktion' fuer
// tridiagonale Matrizen gemaess Glg. (7.43).
// Die Groesse der Matrix (n) und die Vektoren a, b und c sind
// global definiert.
{
int i;
double x1,x2,x;
if(n <= 2) {
printf("Grad zu klein\n");
return 0.0;
}
else {
x2=-(b[n]-lam)/a[n];
x1=-((b[n-1]-lam)*x2 + c[n-1])/a[n-1];
for(i=n-2;i>1;i--){
x= -((b[i]-lam)*x1 + c[i]*x2)/a[i];
x2=x1;
x1=x;
}
return (b[1]-lam)*x1 + c[1]*x2;
}
}
#include "intsch.c"
/*********************** main program *******************/
void main()
{
int anzmax=100;
double *nullst;
.
.
n=....; //Groesse der Matrix
a=dvector(1,n);
b=dvector(1,n);
c=dvector(1,n);
nullst=dvector(1,n);
// Einlesen der Vektoren a b c der tridiagonalen Matrix:
.
.
// Eingabe der INTSCH-Parameter:
anf=....; // Beginn des Grobsuch-Bereichs
aend=....; // Ende des Grobsuch-Bereichs
h=....; // Schrittweite im Grobsuch-Bereich
gen=....; // rel. Genauigkeit der Eigenwerte
intsch(&hymtri,anf,aend,h,gen,anzmax,nullst,&anz);
// Ausgabe der Nullstellen = Eigenwerte der tridiag. Matrix:
.
.
free_dvector(a,1,n);
free_dvector(b,1,n);
free_dvector(c,1,n);
free_dvector(nullst,1,n);
}
Anmerkung: Das Nullstellen-Suchprogramm INTSCH wird im
Abschnitt 5.5.2 genau erklärt. Der im obigen Beispiel angegebene Aufruf
von INTSCH enthält jedoch noch einen zusätzlichen Parameter, nämlich
den aktuellen Namen der Funktion, deren Nullstellen von INTSCH eruiert
werden sollen. Im konkreten Fall ist das die 'Hyman-Funktion' für
tridiagonale Matrizen mit dem Namen 'hymtri'.
Eine solche Möglichkeit, auch Namen von Routinen über Parameterlisten
zu übergeben, bieten viele Programmiersprachen (C, F90, Matlab, ...).
Im Falle eines C-Programms müßten Sie die Headline von INTSCH wie folgt
schreiben:
void intsch(double (*fct)(double),double anf, double aend, double h,
double gen, int anzmax, double nullst[], int *anz)
Zusätzlich müßten Sie im Programm INTSCH jeden Aufruf der Funktion
anpassen:
anstatt ... fct(x) ... ... (*fct)(x) ...
/usr/local/numeric/numrec/c (oder fortran-77 oder fortran-90);
reelle Matrix C/F77/F90
-------------------------------------------------------
Jacobi-Verfahren symm. jacobi
Householder symm. tred2
QL symm.,tridiag. tqli
Balancing general balanc
Reduction to Hessenberg general elmhes
Eigenvalues Hessenb. hqr
(Anmerkung: die Programme 'tred2', 'tql1', 'balanc',
'elmhes' und 'hqr' entstammen der EISPACK-Bibliothek)
-------------------------------------------------------
Mises-Verfahren (betragsgroesster Eigenwert und -vektor:
fmises.c eigval.f90 eigval.for
Verfahren von Martin, Parlett, Peters, Reinsch, Wilkinson
(alle Eigenwerte und -vektoren, QR-Methode):
feigen.c eigen.f90 eigen.for
/usr/local/numeric/num_alg/c/ansic/ansic/07 ('07' bedeutet: Kap. 7)
/usr/local/numeric/num_alg/f77/f77/kap07
/usr/local/numeric/num_alg/f77/f90/kap07
MATLAB Help -- MATLAB Function Listed by Category -- Mathematics -- Linear Algebra -- Eigenvalues and Singular ValuesSie erhalten dann die folgende Liste von Funktionen:
![\includegraphics[scale=0.6]{num7_fig/matlist}](img64.png)
Alle in dieser Liste enthaltenen Funktionen verwenden LAPACK-Programme! Durch Anklicken der entsprechenden Namen (besonders wichtig sind die Funktionen eig und eigs) erhalten Sie genaue Informationen, insbesondere über die Parameterliste.
![\includegraphics[scale=0.9]{num7_fig/nag}](img65.png)