Numerische Methoden zur Lösung von gewöhnlichen Differentialgleichungen: Anfangswertprobleme.

Allgemeines.

Das Auffinden von Lösungen von Differentialgleichungen (Dgl.en) gehört zu den wichtigsten Aufgaben der numerischen Mathematik, und zwar aus zwei Gründen:

• Obwohl es eine ganze Reihe von analytischen Methoden zur Lösung von Dgl.en gibt, sind analytische Lösungen häufig sehr kompliziert und so aufwendig zu ermitteln, daß es oft nicht dafür steht. Dies soll aber die Bedeutung von analytischen Methoden keineswegs herabsetzen. Das Motto aus dem Numerik-Buch von Dorn/McCracken [7] 'Numerical methods are no excuse for poor analysis' gilt auch hier.
• Für eine ganze Reihe von Dgl.en gibt es überhaupt keine geschlossen darstellbaren analytischen Lösungen. Dies ist zum Beispiel bei der relativ 'harmlos' aussehenden Dgl.
  
  $$y'(x)=x^{2}+y(x)^{2}$$
  
  
  der Fall! In solchen Fällen ist nur eine numerische Lösung möglich.

Im folgenden wird ausschließlich von expliziten Dgl.en die Rede sein, d.h. von solchen, die nach der jeweils höchsten vorkommenden Ableitung aufgelöst werden können. Dgl.en von der Art

$$y'(x) + \log y'(x) = 1$$

werden also in diesem Abschnitt nicht behandelt. Außerdem funktionieren die im weiteren zu behandelnden Verfahren nur für Dgl.en bzw. für Systeme von Dgl.en erster Ordnung. Diese Einschränkung ist jedoch bedeutungslos, da ja jede explizite Dgl. höherer Ordnung in ein äquivalentes System von Dgl.en erster Ordnung umgewandelt werden kann.
So ist die Dgl. n-ter Ordnung

$$y^{(n)} = F(x;y,y',y'',\ldots,y^{(n-1)})$$

äquivalent mit dem System

$$\begin{array}{ll} y_{1}'=y_{2} & \equiv f_{1}(x) \\ y_{2... ...'=F(x;y_{1},y_{2},\ldots,y_{n}) & \equiv f_{n}(x) \end{array}$$

Faßt man die Größen $y_{i}'$, $y_{i}$ und $f_{i}$ als Vektor-Komponenten auf, so kann ein solches System in der Form

$${\bf y}'(x) = {\bf f}(x;{\bf y})$$ (8.1)

geschrieben werden.

Alle numerischen Verfahren zur näherungsweisen Lösung von Dgl.en liefern natürlich keine Funktionen mit allgemeinen Integrationskonstanten, sondern berechnen punktweise jene Lösungen, die durch die entsprechenden Nebenbedingungen spezifiziert werden. In diesem Kapitel werden nur Anfangswert-Probleme behandelt, d.h. solche, bei denen die Nebenbedingungen das Verhalten der Lösungsfunktionen ${\bf y}(x)$ in einem Punkt $x=x_{o}$ festlegen. Ein vollständig definiertes Anfangswert-Problem hat daher die Form

$${\bf y}'(x) = {\bf f}(x;{\bf y}) \qquad \mbox{mit} \quad {\bf y}(x_{o})= {\bf y}_{o} \quad .$$ (8.2)

Eine Taylorreihenentwicklung der Lösungsfunktionen.

Ausgangspunkt aller weiteren Überlegungen ist die Potenzreihenentwicklung der i-ten Lösungsfunktion des Systems (8.2)

$$y_{i}(x)=\sum_{\nu =0}^{p} \frac{(x-x_{o})^{\nu}}{\nu !} \le... ...^{\nu}}{dx^{\nu}} y_{i}(x)\right]_{x_{o},{\bf y}_{o}} + R_{i}$$ (8.3)

mit dem Lagrange'schen Restglied

$$R_{i}=\frac{(x-x_{o})^{p+1}}{(p+1)!} \left[\frac{d^{p+1}}{dx... ...} y_{i}(x) \right]_{x=\xi} \qquad x_{o}\leq \xi \leq x \quad .$$ (8.4)

Der Zweck aller folgenden Verfahren besteht nun darin, ausgehend von dem Anfangspunkt des Dgl.ssystems $x_{o}$ einen Näherungswert für die $y_{i}$ an der Stelle $x_{o}+h$ zu berechnen. Dabei nennt man $p$ die Ordnung des Verfahrens:

$$\hat y_{i}(x_{o}+h)=\sum_{\nu=0}^{p} \frac{h^{\nu}}{\nu !} \... ...^{\nu}}{dx^{\nu}} y_{i}(x) \right]_{x_{o},{\bf y}_{o}} \quad .$$ (8.5)

Anmerkung: Hier und im folgenden werden Näherungswerte von $y$ stets mit $\hat y$ bezeichnet.

Die Methode von Euler.

Die älteste Näherungsmethode zur numerischen Behandlung von Dgl.ssystemen stammt von Leonhard Euler. In diesem Verfahren erster Ordnung ($p$=1) wird die Entwicklung (8.5) bereits nach dem zweiten Term abgebrochen, und man erhält

$$\hat y_{i}(x_{o}+h)=y_{i}(x_{o})+h \cdot y'(x)\mid_{x=x_{o}} = y_{i}(x_{o}) + h \cdot f_{i}(x_{o},{\bf y}_{o})$$ (8.6)

Die geometrische Interpretation dieser Formel ist denkbar einfach: Es wird die exakte Lösung $y_{i}(x)$ durch deren Tangente im Anfangspunkt $x_{o}$ angenähert (s. Abb. 8.1).
Es leuchtet ein, daß die Euler'sche Methode nur für sehr kleine Schrittweiten brauchbare Resultate liefert.

Abbildung 8.1: Geometrische Interpretation der Methode von Euler.

Die Runge-Kutta-Methoden.

Runge-Kutta-Methoden sind die weitaus populärsten zur numerischen Behandlung von Anfangswertproblemen, vor allem deshalb, weil sie sich außerordentlich gut für die Rechenmaschine eignen und in vielen Fällen Resultate hoher Genauigkeit mittels akzeptablen Rechenaufwandes liefern.
Der - wie noch zu erläutern sein wird - größte Nachteil der Runge-Kutta-Methoden liegt in der ziemlich schwierigen Fehlerabschätzung (s. Abschnitt 8.4.5).

Runge-Kutta-Methoden sind durch die folgenden drei Prinzipien charakterisiert:

• Sie leiten sich aus Taylorreihen der gesuchten Lösungsfunktionen ab, die nach dem Term mit $h^{p}$ abgebrochen werden. $p$ ist die Ordnung der jeweiligen Runge-Kutta-Methode.
• Sie sind sogenannte Einschritt-Verfahren, d.h. zur Berechnung von Näherungswerten an der Stelle $x+h$ genügt die Information über den vorhergehenden Punkt $x$.
• Zur Berechnung der Näherungswerte für die $y_{i}(x)$ werden nur die gegebenen Funktionen $f_{i}(x,{\bf y})$ benötigt, nicht aber deren Ableitungen! Dies ist in der Praxis ein wichtiger Vorteil gegenüber der Taylorreihen-Entwicklung.

Aus diesen drei Charakteristiken für Runge-Kutta-Methoden ergibt sich sofort:

Die Methode von Euler ist eine Runge-Kutta-Methode erster Ordnung.

Runge-Kutta-Methoden zweiter Ordnung.

Es soll nun gezeigt werden, wie Runge-Kutta-Formeln zweiter Ordnung gewonnen werden können. Der Einfachheit halber wird hier ein 'Dgl.ssystem' behandelt, das nur aus der einzigen Gleichung

$$y'(x)=f(x,y)$$

mit der Anfangsbedingung

$$y(x_{o})=y_{o}$$

besteht. Ausgangspunkt für eine Runge-Kutta-Formel 2. Ordnung ist der Ansatz

$$\hat y(x_{o}+h)=y_{o}+h\cdot (c_{1} g_{1} + c_{2} g_{2}) \quad .$$ (8.7)

In (8.7) stellen die Größen $g_{1}$ und $g_{2}$ Funktionswerte von $f(x,y)$ dar, und zwar

$$\begin{array}{lll} g_{1} & = & f(x_{o},y_{o}) \\ g_{2} & = & f(x_{o}+a_{2} h,y_{o}+b_{2,1} h g_{1}) \end{array}$$ (8.8)

$c_{1}$, $c_{2}$, $a_{2}$ und $b_{2,1}$ sind die Runge-Kutta-Koeffizienten. Diese sind so zu wählen, daß der obige Ansatz mit dem Taylorreihen-Ansatz (8.5) für $p=2$

$$\hat y(x_{o}+h) = y_{o} + h \cdot f(x_{o},y_{o}) + \frac{h^{2}}{2} \left[ f_{x} + f \cdot f_{y} \right]_{x_{o},y_{o}}$$ (8.9)

(näherungsweise) identisch wird.
Dazu entwickelt man $g_{2}$ (8.8) an der Stelle $h=0$ nach Potenzen von $h$ und bricht diese Entwicklung nach dem linearen Term ab:

$$g_{2}(h) = g_{2}(h=0) + h \cdot \left[ \frac{d}{dh} g_{2}(h) \right]_{h=0}$$ (8.10)

$$= f(x_{o},y_{o}) + h \cdot \left[ f_{x}(x_{o},y_{o}) \cdot a_{2} + f(x_{o},y_{o}) \cdot f_{y}(x_{o},y_{o}) \cdot b_{2,1} \right]$$

Setzt man nun (8.10) zusammen mit $g_{1}=f(x_{o},y_{o})$ in den Runge-Kutta-Ansatz (8.7) ein, so ergibt sich weiter

$$\hat y(x_{o}+h) = y_{o} + h\cdot c_{1} \cdot f(x_{o},y_{o}) + h \cdot c_{2} \cdot f(x_{o},y_{o}) +$$ (8.11)

$$+h^{2} \cdot c_{2} \cdot a_{2} \cdot f_{x}(x_{o},y_{o}) + h^{2} \cdot c_{2} \cdot b_{2,1} \cdot f(x_{o},y_{o}) \cdot f_{y}(x_{o},y_{0}) \quad .$$

Durch Gleichsetzen von (8.9) und (8.11) und einen Koeffizientenvergleich bzgl. der Größen $f$, $f_{x}$ und $f\cdot f_{y}$ erhält man das folgende nicht-lineare Gleichungssystem für die gesuchten Runge-Kutta-Koeffizienten zweiter Ordnung:

$$c_{1} + c_{2} = 1$$

$$c_{2} \cdot a_{2} = \frac{1}{2}$$ (8.12)

$$c_{2} \cdot b_{2,1} = \frac{1}{2}$$

Dieses System ist jedoch unterbestimmt: vier zu ermittelnden Koeffizienten stehen nur drei Gleichungen gegenüber! Es kann also einer der vier Koeffizienten frei gewählt werden. Die Konsequenz daraus ist, daß es nicht nur eine Runge-Kutta-Methode zweiter Ordnung gibt, sondern unendlich viele, wobei es von der Geschicklichkeit des Rechnenden abhängt, einen Koeffizienten so zu wählen, daß die übrigen drei Werte möglichst einfach werden.

Dazu zwei Beispiele:

• Mit der Wahl $c_{1}=0$ erhält man für
  
  $$c_{2}=1 \qquad a_{2}=\frac{1}{2} \qquad \mbox{und} \qquad b_{2,1}= \frac{1}{2} \quad .$$
  
  
  Die aus (8.7) resultierende Runge-Kutta-Formel
  

  $$\hat y(x_{o}+h)=y_{o} + h\cdot f(x_{o}+\frac{h}{2}, y_{o}+\frac{h}{2} f(x_{o},y_{o}))$$ (8.13)

  
  
  wird modifizierte Euler'sche Methode genannt.
• Mit der Wahl $c_{1}=1/2$ erhält man hingegen
  
  $$c_{2}=\frac{1}{2} \qquad a_{2}=1 \qquad b_{2,1}=1 \quad .$$
  
  
  Die entsprechende Lösung
  

  $$\hat y(x_{o}+h) = y_{o} + h \left\{ \frac{1}{2} f(x_{o},y_{o... ...ac{1}{2} f\left[x_{o}+h,y_{o}+h f(x_{o},y_{o})\right] \right\}$$ (8.14)

  
  
  heißt verbesserte Euler'sche Methode.

Die grafische Interpretation dieser beiden Näherungsformeln geht aus der Abb.8.2 hervor.

• modifizierte Euler-Formel: Die Lösungsfunktion wird angenähert durch eine Gerade durch $(x_{o},y_{o})$ mit der Steigung von $y(x)$ im Mittelpunkt des Intervalls $\left[ x_{o},x_{o}+h \right]$.
• verbesserte Euler-Formel: Die Lösungsfunktion wird angenähert durch eine Gerade durch $(x_{o},y_{o})$, deren Steigung das arithmetische Mittel aus $y'(x_{o})$ und $\hat y'(x_{o}+h)$ ist.

Abbildung 8.2: Grafische Interpretation der 'modifizierten Euler-Formel' (links) und der 'verbesserten Euler-Formel' (rechts).

Im Diagramm 8.3 werden die bisher vorgestellten Runge-Kutta-Formeln (8.6), (8.13) und (8.14) auf das einfache Beispiel

$$y'(x)=e^{x} \qquad y(0)=0$$

angewendet. Die exakte Lösung ist

$$y(x)=e^{x}-1 \quad ,$$

und gesucht ist $\hat y(1)$.

Abbildung 8.3: Ein Testbeispiel für Runge-Kutta-Methoden erster und zweiter Ordnung.

Aus den in Abb. 8.3 dargestellten Ergebnissen geht klar hervor, daß die beiden Runge-Kutta-Methoden zweiter Ordnung eine Klasse besser sind als das einfache Euler-Verfahren erster Ordnung.
Es wäre hingegen falsch, aus der Tatsache, daß beim gegebenen Beispiel die 'modifizierte Euler-Formel' den exakten Lösungswert besser approximiert als die 'verbesserte Euler-Formel', zu schließen, daß erstere Methode besser ist als letztere. Dies ist reiner Zufall und kann bei einem anderen Beispiel umgekehrt sein!

Jede Runge-Kutta-Formel derselben Ordnung ist prinzipiell gleichwertig!

Runge-Kutta-Methoden höherer Ordnung.

Für Dgl.ssysteme von $n$ Gleichungen lautet der allgemeine Runge-Kutta-Ansatz $p$-ter Ordnung:

$$\hat y_{i}(x_{o}+h)=y_{i,o} + h \cdot \sum_{j=1}^{p} c_{j} g_{i,j}$$ (8.15)

mit

$$g_{i,1}=f_{i}(x_{o};y_{1,o},y_{2,o},\ldots,y_{n,o})$$ (8.16)

und

$$g_{i,j} = f_{i}(x_{o}+a_{j}h;y_{1,o}+h\sum_{\ell =1}^{j-1} b_{j,\ell} g_{1,\ell},\ldots,$$

$$y_{n,o}+h\sum_{\ell =1}^{j-1} b_{j,\ell} g_{n,\ell})$$ (8.17)

mit $i=1,\ldots,n$ und $j=1,\ldots,p$.

[(8.17) ist offenbar eine Rekursionsformel: Zur Berechnung der $g_{i,j}$ ist die Kenntnis aller vorherigen $g$-Werte $g_{k,\ell}$, $\ell=1,\ldots,j-1$ und $k=1,\ldots,n$ erforderlich.]

Der Runge-Kutta-Ansatz (8.15) enthält genau $(p^{2}+3p-2)/2$ Koeffizienten, und zwar

• die $p$ Werte $\qquad c_{1},\ldots,c_{p}\quad$,
• die $p-1$ Werte $\qquad a_{2},\ldots,a_{p}\quad$ und
• die $p(p-1)/2$ Werte $\qquad b_{2,1},\ldots,b_{p,p-1}\quad$.

Zur besseren Übersichtlichkeit können diese Koeffizienten auch als Schema der Art

geschrieben werden. Die Berechnung der Koeffizienten erfolgt im Prinzip gleich wie für den Fall $p=2$. Für größere Werte von $p$ wird die Rechnung jedoch ziemlich umfangreich (s. z.B. [19]). In jedem Fall ergeben sich aber für die Koeffizienten unterbestimmte Gleichungssysteme, was auch für $p>2$ zu einer unendlichen Mannigfaltigkeit von Runge-Kutta-Formeln führt.

Natürlich braucht der Benutzer diese Formeln nicht selbst abzuleiten, sondern er kann sie der Literatur entnehmen. Eine Sammlung von Runge-Kutta-Formeln der Ordnungen 1-8 ist z.B. in [2], S. 215-217, zu finden.

In der Praxis werden heute hauptsächlich Runge-Kutta-Methoden vierter Ordnung angewendet, darunter vor allem

die 3/8-Formel:                     die 'klassische'
                                    Runge-Kutta-Formel:

Das im Abschnitt 8.5 präsentierte Programm beruht auf der klassischen Runge-Kutta-Formel. Aus diesem Grund seien die entsprechenden Formeln nun explizite hingeschrieben:

$$\hat y_{i}(x_{o}+h)=y_{i,o}+h\left[ \frac{1}{6} g_{i,1}+\fra... ...3} g_{i,2} + \frac{1}{3} g_{i,3} + \frac{1}{6} g_{i,4} \right]$$ (8.18)

mit

$$g_{i,1} = f_{i}(x_{o};y_{1,o},\ldots,y_{n,o})$$

$$g_{i,2} = f_{i}(x_{o}+\frac{h}{2};y_{1,o}+\frac{h}{2} g_{1,1},\ldots, y_{n,o}+\frac{h}{2} g_{n,1})$$ (8.19)

$$g_{i,3} = f_{i}(x_{o}+\frac{h}{2};y_{1,o}+\frac{h}{2} g_{1,2},\ldots, y_{n,o}+\frac{h}{2} g_{n,2})$$

$$g_{i,4} = f_{i}(x_{o}+h;y_{1,o}+h g_{1,3},\ldots, y_{n,o}+h g_{n,3})$$

und $i=1,\ldots,n$. Wie man sieht, hat die Tatsache, daß die Koeffizienten $b_{3,1}$, $b_{4,1}$ und $b_{4,2}$ Null sind, die angenehme Konsequenz, daß die in (8.17) auftretenden Summen zu einem Term reduziert werden.

Anmerkung: Das klassische Runge-Kutta-Verfahren würde, auf das Beispiel von Seite 240 angewendet, einen Fehler von lediglich $=0.034 \%$ ergeben.

Die Anwendung von Runge-Kutta-Formeln.

Die Formeln (8.18) und (8.19) dienen also dazu, ausgehend von bekannten Anfangswerten $y_{i,o}$ an der Stelle $x=x_{o}$ Näherungswerte für die Lösungsfunktionen an der Stelle $x=x_{o}+h$ zu berechnen.

Nun ist man aber i.a. nicht nur an den Näherungslösungen für den einen Abszissenwert $x_{1}=x_{o}+h$ interessiert, sondern auch an den $\hat y_{i}$ für die weiteren Abszissenwerte $\cdots x_{4}>x_{3}>x_{2} >x_{1}$! Das heißt aber, daß das Runge-Kutta-Verfahren nicht nur einmal angewendet wird, sondern oftmals hintereinander, wobei man sich Schritt für Schritt vom Anfangspunkt $x_{o}$ wegbewegt:

$$\hat y_{i}(x_{o}+h)\equiv \hat y_{i,1} = y_{i,o} + h\sum_{j=1}^{p} c_{j} g_{i,j}(x_{o};y_{1,o},\ldots,y_{n,o})$$

$$\hat y_{i}(x_{o}+2h)\equiv \hat y_{i,2} = \hat y_{i,1} + h\su... ...^{p} c_{j} g_{i,j}(x_{o}+h;\hat y_{1,1},\ldots,\hat y_{n,1})$$

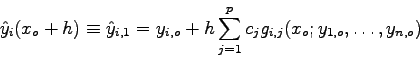
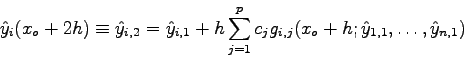
Der wesentliche Unterschied zwischen dem ersten und allen weiteren Runge-Kutta-Schritten besteht darin, daß die $x/y$-Werte auf der rechten Seite der ersten Gleichung die exakt bekannten Anfangswerte des gegebenen Problems sind, während die $x/y$-Werte der folgenden Gleichungen nur Näherungswerte darstellen!

Ein Testbeispiel: Qualitätsprobleme.

Es soll nun angenommen werden, daß ein Programm RUNGETEST vorliegt, mit Hilfe dessen ein Anfangswertproblem (8.2) mittels der Formeln (8.18), (8.19) gelöst werden kann, wobei die (vom Benutzer festgelegte) Schrittweite $h$ während des ganzen Runge-Kutta-Prozesses konstant ist.
Die Leistungsfähigkeit von RUNGETEST soll im folgenden an Hand eines durchaus nicht-trivialen Problems getestet werden: Es geht dabei um die Bahnkurve eines Erdsatelliten (s. Abb. 8.4).

Abbildung 8.4: Bahnkurve eines Erdsatelliten.

Definition des Problems:

Ein Satellit wird von der Oberfläche der Erde tangential mit der Geschwindigkeit $v_{max}$ in Bewegung gesetzt. Zu berechnen ist seine Bahnkurve unter den folgenden Bedingungen bzw. Idealisierungen:

• $v_{max} <$ Fluchtgeschwindigkeit.
• Die Erde sei eine homogene, ideale Kugel mit dem Radius $r_{min}$.
• Vernachlässigung des Einflusses der Lufthülle der Erde.
• Vernachlässigung des Einflusses aller anderen Himmelskörper.

Unter diesen Voraussetzungen lautet die Bewegungsgleichung des Satelliten

$$\ddot {\bf r} = -\frac{\gamma M}{r^{3}} {\bf r}$$ (8.20)

mit der Gravitationskonstanten $\gamma=6.67 \cdot 10^{-11}$ $m^{3}/kgs^{2}$ und
der Masse der Erde $M=5.977 \cdot 10^{24}$ $kg$. ${\bf r}$ ist der Radiusvektor vom Erdmittelpunkt zur momentanen Satelliten-Position.
Die Gleichung (8.20) führt letztlich zum folgenden System von 2 Dgl.en zweiter Ordnung für (1) den Abstand $r$ und (2) den Drehwinkel $\varphi$:

$$\ddot r = r \dot \varphi^{2} - \frac{\gamma M}{r^{2}}$$

$$\ddot \varphi = -\frac{2\dot r \dot \varphi}{r}$$ (8.21)

Setzt man

$$r \rightarrow y_{1} \quad \varphi \rightarrow y_{2} \quad \d... ...\rightarrow y_{3} \quad \dot \varphi \rightarrow y_{4} \quad ,$$

erhält man daraus das folgende System von 4 Dgl.en erster Ordnung:

$$\dot y_{1} = y_{3} \qquad y_{1}(t=0) = r_{min}$$

$$\dot y_{2} = y_{4} \qquad y_{2}(t=0) = 0$$

$$\dot y_{3} = y_{1} y_{4}^{2} - \frac{\gamma M}{y_{1}^{2}} \qquad y_{3}(t=0) = 0$$ (8.22)

$$\dot y_{4} = -\frac{2y_{3}y_{4}}{y_{1}} \qquad y_{4} = \frac{v_{max}}{r_{min}} = 58.29527$$

Für die konkreten Testläufe war $r_{min}=6.37 \cdot 10^{6}$ $m$ und $v_{max}=10.4 \cdot 10^{3}$ $m/s$.

Wenn man nun alle Längen in Einheiten $r_{min}$ mißt, alle Geschwindigkeiten in Einheiten $v_{max}$, und alle Zeiten in Einheiten der (theoretisch berechenbaren) exakten Umlaufzeit, ergibt sich für den in Glg. (8.21) vorkommenden Faktor

$$\alpha \equiv \gamma M = 1966.39 .$$

Ein entscheidendes Kriterium für die Zuverlässigkeit der numerischen Methode ist natürlich die Bahnstabilität, d.h. die Bahnellipse sollte sich Umlauf für Umlauf exakt wiederholen. Jede Abweichung von dieser Stabilität deutet auf Verfahrens- und/oder Rundungsfehler^8.1 im Runge-Kutta-Programm hin!
Es leuchtet unmittelbar ein, daß die Verfahrensfehler des Programmes umso kleiner sein werden, je kleiner man die Schrittweite des Runge-Kutta-Prozesses wählt. Diese Tatsache ist in der Abbildung 8.5 eindrucksvoll zu sehen, wo jeweils 5 volle Umläufe dargestellt sind. Die verwendeten Schrittweiten waren (a) $1/50$, (b) $1/60$, (c) $1/70$ und (d) $1/80$ der Umlaufzeit des Satelliten.
Diese Testergebnisse zeigen deutlich, welch großen Einfluß die Schrittweite auf die performance des Runge-Kutta-Prozesses hat: Bei einer Schrittweite von $1/50$ der Umlaufzeit (a) ist der Prozess vollkommen instabil, während bei einer Schrittweite, die nur um einen Faktor $1.6$ kleiner ist (d), eine fast perfekte Bahnstabilität vorliegt.

Man kann also sagen:

• Das Programm RUNGETEST ist für die Praxis ungeeignet!
• Jedes praktisch verwendbare Runge-Kutta-Programm muß unbedingt über eine Fehlerdiagnostik bzw. eine damit verbundene automatische Schrittweitensteuerung verfügen!

Abbildung 8.5: Ein Stabilitätstest für RUNGETEST. Die konstanten Schrittweiten wurden wie folgt gewählt: (a) $h=1/50$, (b) $h=1/60$, (c) $h=1/70$, (d) $h=1/80$ der Umlaufzeit. Der Stern markiert den Erdmittelpunkt, und die punktierte Linie stellt die analytisch berechnete, exakte Ellipsenbahn des Satelliten dar.

Fehlerabschätzung und Schrittweiten-Steuerung beim Runge-Kutta-Verfahren.

Wie schon oft erwähnt, wird ein numerisches Ergebnis erst durch die Angabe seines (absoluten oder relativen) Fehlers brauchbar. Man hätte ja ansonsten keinerlei Anhaltspunkte für die Qualität des Näherungsergebnisses.

Da die Runge-Kutta-Methoden eng mit dem Taylorreihen-Ansatz (8.3) verwandt sind, liegt es nahe, das entsprechende Restglied von Lagrange (8.4) zur Abschätzung des Verfahrensfehlers heranzuziehen. Für das klassische Runge-Kutta-Verfahren (Ordnung $p=4$) ergibt sich daraus

$$E_{V} = \frac{h^{5}}{120} \left[ y_{i}^{(5)}(x) \right]_{x=\xi} \qquad x_{o}\leq \xi \leq x_{o}+h$$

bzw.

$$E_{V} = C(h) \cdot h^{5} \quad .$$ (8.23)

Da aber $E_{V}$ den Fehler zwischen dem exakten Wert der Lösungsfunktion $y_{i}(x)$ an der Stelle $x_{o}+h$ und der entsprechenden Näherungslösung $\hat y_{i}(x_{o}+h)$ darstellt, gilt weiter

$$y_{i}(x_{o}+h) = \hat y_{i}(x_{o}+h) + C(h) \cdot h^{5} \quad .$$ (8.24)

Ebenso kann man aber, um von $x_{o}$ nach $x_{o}+h$ zu gelangen, nacheinander zwei Runge-Kutta-Schritte mit der Schrittweite $h/2$ machen. Dies ergibt

$$y_{i}(x_{o}+h) = \hat y_{i}(x_{o}+2\cdot \frac{h}{2}) + C(h/2) \cdot 2 \cdot \left( \frac{h}{2} \right)^{5} \quad .$$ (8.25)

Im weiteren soll nun der Index $i$ bei den $y$-Werten weggelassen werden, und außerdem werden die Abkürzungen

$$\hat y(x_{o}+h) \equiv \hat y(h) \qquad \mbox{und} \qquad \hat y(x_{o}+2 \frac{h}{2}) \equiv \hat y(h/2)$$

eingeführt. Wenn man nun annimmt, daß die $h$-Abhängigkeit der Größe $C$ nicht allzu groß ist, daß also in guter Näherung

$$C(h) \approx C(h/2) = C$$

ist, kann man diese Konstante (und damit den Verfahrensfehler
$E_{V}(h)=C h^{5}$) durch Gleichsetzen von (8.24) und (8.25) berechnen:

$$E_{V}(h) = \frac{16}{15} \left[\hat y(h/2) - \hat y(h)\right] \approx \hat y(h/2) - \hat y(h) \quad .$$ (8.26)

D.h.: Die Differenz zwischen den beiden Runge-Kutta-Ergebnissen $\hat y(h/2)$ (= Näherungsergebnis nach 2 Halbschritten) und $\hat y(h)$ (= Näherungsergebnis nach 1 Ganzschritt) kann approximativ mit dem auftretenden (absoluten) Verfahrensfehler gleichgesetzt werden.

Aus der Kombination der Gleichungen (8.25) und (8.26) folgt auch sofort eine Beziehung, die es erlaubt, die erhaltenen Näherungswerte $\hat y$ auf einfache Weise zu verbessern:

$$\hat y_{verbessert} = \hat y(h/2) + \frac{\hat y(h/2)-\hat y(h)}{15} .$$ (8.27)

Diese Korrektur hat jedoch ein Problem: man erhält zwar (i. a.) einen deutlich verbesserten Näherungswert für die Lösungsfunktion $y$, hat aber keinerlei Information über die Qualität dieses korrigierten $y$! Aus diesem Grund wird in vielen Programmen auf die Anwendung der obigen Formel verzichtet.

Nun kommt der entscheidende Punkt: Man kann sich die Frage stellen, wie groß die ideale Schrittweite $h$ hätte sein müssen (oder sein dürfen), um zu gewährleisten, daß $E_{V}$ eine vorgegebene Fehlerschranke $\epsilon$ gerade nicht überschreitet.
Da aber der Verfahrensfehler mit der fünften Potenz von $h$ variiert, ist diese Frage leicht zu beantworten. Es gilt einfach:

$$\frac{\epsilon}{E_{V}(h)} = \left( \frac{h_{ideal}}{h} \right)^{5}$$

Daraus erhält man sofort eine Bestimmungsgleichung für $h_{ideal}$:

$$h_{ideal} = h \cdot \left( \frac{\hat y(h/2)-\hat y(h)}{\epsilon} \right)^{-\frac{1}{5}}$$ (8.28)

Diese Gleichung ist die Basis für eine Schrittweitensteuerung, wie sie im Programm RKQC (Abschnitt 8.5.2) verwendet wird. Dabei wird der aktuelle Verfahrensfehler gemäß (8.26) berechnet und mit der Fehlerschranke $\epsilon$ verglichen. Die weitere Vorgangsweise ist die folgende:

• $\epsilon \geq \hat y(h/2)-\hat y(h)$: Der Fehler des letzten Runge-Kutta-Schrittes ist kleiner als $\epsilon$. Für den nächsten Runge-Kutta-Schritt kann daher die Schrittweite gemäß (8.28) vergrößert werden.
• $\epsilon < \hat y(h/2)-\hat y(h)$: Der Fehler des letzten Runge-Kutta-Schrittes ist größer als $\epsilon$. Die Schrittweite wird gemäß (8.28) verkleinert und der letzte Runge-Kutta-Schritt wird wiederholt.

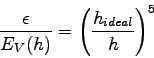
Mit dieser Strategie wird zweierlei erreicht: Zum ersten ist gewährleistet, daß die Schrittweite stets klein genug ist, um den jeweiligen (lokalen) Verfahrensfehler unter der geforderten Grenze $\epsilon$ zu halten, zum zweiten wird aber stets mit einer möglichst großen Schrittweite gearbeitet, was sich auf die Rechenzeit positiv auswirkt.

Abschließend soll noch einmal darauf hingewiesen werden, daß die hier vorgestellte Methode der Schrittweitensteuerung auf einer Reihe von Annahmen basiert (etwa der Annahme der Unabhängigkeit der Größe $C$ von $h$), die durchaus nicht immer erfüllt sein müssen! Zusätzlich wird hier immer nur der lokale Fehler berücksichtigt, und dabei außer acht gelassen, daß sich in vielen Fällen die von Schritt zu Schritt auftretenden lokalen Fehler zu einem viel drastischeren globalen Fehler aufsummieren können.

Die Schrittweitensteuerung, die im nun folgenden Programm verwendet wird, versucht auf einige dieser Probleme Rücksicht zu nehmen.

Die Programme ODEINT, RKQC und RK4.

Quelle: [9], S. 550-560, vereinfacht.

Die Programme ODEINT, RKQC und RK4 dienen zur numerischen Auswertung eines Anfangswertproblems (8.1).

Das Programm ODEINT.

ODEINT (Ordinary Differential Equations INTegrator) ist das 'driver program' des Programmsystems:

INPUT-Parameter:

YSTART( ):

Vektor ${\bf y}_{o}$ der Anfangswerte des Dgl.ssystems.

N:

Anzahl $n$ der Gleichungen des Systems.

X1, X2:

Startpunkt und Endpunkt des Integrationsintervalls.

EPS:

Geforderte relative Genauigkeit (s. die folgenden Anmerkungen).

HANF:

Guessed value für die Schrittweite des Runga-Kutta-Prozesses.

HMIN:

Minimalwert, unter den die Arbeitsschrittweite nicht sinken darf.

NSTMAX:

Maximale Anzahl von Stützpunkten, die in den Feldern XX bzw. YY abgespeichert werden kann.

OUTPUT-Parameter:

NWERTE:

Anzahl der abgespeicherten Stützpunkte.

XX( ):

Abszissenwerte der Stützpunkte.

YY( , ):

Ordinatenwerte der Lösungsfunktionen:
erster Index = Index der Funktion,
zweiter Index = Kennzeichnung des Abszissenwertes.

Anmerkungen zu ODEINT:

Dieses Programm kontrolliert die schrittweise Abarbeitung des Runge-Kutta-Prozesses im Bereich X1$\leq$X$\leq$X2. Die (von der Routine RKQC gelieferten) qualitäts-kontrollierten Ergebnisse an den Stützpunkten werden auf den Feldern XX und YY abgespeichert. Auf die Zahl und die Verteilung dieser Werte im Intervall [X1,X2] hat man keinen Einfluß.
Die Näherungswerte $\hat y_{i}$ für das Ende des Integrationsintervalls (X2) werden zusätzlich über das Feld YSTART an das aufrufende Programm zurückgegeben. Dies ist praktisch für den Fall, daß diese $\hat y_{i}$-Werte als Anfangswerte für ein weiteres, unmittelbar anschließendes Integrationsintervall dienen sollen.
Eine weitere wichtige Aufgabe von ODEINT besteht in der Berechnung der Skalierungswerte für die Fehlerdiagnostik. Da mit EPS eine relative Fehlerschranke gemeint ist, wäre es sinnvoll, bzgl. der Beträge der jeweiligen $\hat y_{i}$-Werte zu skalieren, also

YSCAL(I):= |Y(I)|

zu schreiben. Eine solche Skalierung würde aber im Falle einer Nullstelle von $y_{i}$ zu einem Programmabbruch führen (Division durch Null im Programm RKQC); aus diesem Grund wird im Programm ODEINT wie folgt skaliert:

YSCAL(I):= |Y(I)| + |H*F(I)| + 'TINY'      ,

wodurch jede derartige Komplikation ausgeschlossen ist.

Das Programm RKQC.

RKQC (Runge-Kutta Quality Control): Dieses Programm führt die Qualitätskontrolle der einzelnen Runge-Kutta-Schritte und die damit zusammenhängende Schrittweiten-Steuerung durch.

INPUT-Parameter:

Y( ):

$\hat y_{i}$-Werte des letzten Runge-Kutta-Schrittes =
Startwerte für den nächsten Schritt.

F( ):

Feld der entsprechenden $f_{i}$-Werte.

N:

Anzahl der Gleichungen des Dgl.ssystems.

X:

Abszissenwert des aktuellen Startwertes.

HTRY:

Schrittweite für den nächsten Schritt.

EPS:

Geforderte relative Genauigkeit.

YSCAL( ):

Scaling factors für die nächste Genauigkeitsabfrage.

OUTPUT-Parameter:

Y( ):

Neu berechnete $\hat y_{i}$-Werte.

F( ):

Feld der entsprechenden $f_{i}$-Werte.

X:

Neu berechneter Abzissenwert.

HNEXT:

Für den nächsten Schritt vorgeschlagene Schrittweite.

Anmerkungen zu RKQC:

In diesem Programm werden jeweils die drei für die Fehlerdiagnostik erforderlichen Runge-Kutta-Schritte durchgeführt, davon zwei Schritte mit $h/2$ und ein Schritt mit $h$. Danach erfolgt die approximative Berechnung des Verfahrensfehlers gemäß (8.26) für jede Lösungsfunktion $\hat y_{i}$. Der Maximalwert der skalierten Verfahrensfehler wird berechnet und unter ERRMAX abgespeichert. ERRMAX entspricht also dem Ausdruck

$$\mbox{Max}\left[ \mid \hat y(h/2)-\hat y(h)\mid_{rel}\right]$$

im Sinne von (8.26).

Dann erfolgt eine Programmverzweigung: Im Falle von

$$\mbox{ERRMAX} \leq \mbox{EPS}$$

war der Runge-Kutta-Schritt erfolgreich. Nun wird, abgesehen von einer letzten Korrektur der $\hat y$ gemäß (8.27), die ideale Schrittweite für den nächsten Schritt berechnet. Der entsprechende Befehl

$$\mbox{HNEXT}:=\mbox{SAFETY*H*(ERRMAX/EPS)**}(-1.0/5.0)$$

entspricht bis auf die 'Sicherheitskonstante' SAFETY:=0.9 genau der Gleichung (8.28). Allerdings gibt es im Falle sehr kleiner Werte von
ERRMAX noch eine Sicherheitsabfrage^8.2. Um zu verhindern, daß HNEXT zu stark anwächst, wird im Falle

$$\mbox{ERRMAX/EPS} < \mbox{ERRCON}$$

die nächste Schrittweite einfach wie folgt berechnet:

$$\mbox{HNEXT}:=4. * \mbox{H}$$

Dann erfolgt der Rücksprung ins Programm ODEINT.

Im Falle von

$$\mbox{ERRMAX} > \mbox{EPS}$$

war der Runge-Kutta-Schritt nicht erfolgreich und muß daher mit einer kleineren Schrittweite wiederholt werden. Der entsprechende Befehl

$$\mbox{H:=SAFETY*H*(ERRMAX/EPS)**}(-1.0/4.0)$$

unterscheidet sich von (8.28) außer durch SAFETY noch durch einen veränderten Exponenten: dies soll der bereits erwähnten Tatsache Rechnung tragen, daß die globale Fehlerzunahme in manchen Fällen dramatischer verläuft als die lokale Fehlerzunahme. Der gegenüber (8.28) verkleinerte Exponent sorgt in diesem Sinne für noch kleinere Schrittweiten und dementsprechend für eine noch günstigeres Fehlerverhalten des Runge-Kutta-Prozesses.

Die Programme RK4 und DERIVS.

RK4 (Runge-Kutta 4) führt die Auswertung der einzelnen Runge-Kutta-Schritte nach Maßgabe der Gleichungen (8.18) und (8.19) durch:

INPUT-Parameter:

Y( ):

Startwerte für den aktuellen Runge-Kutta-Schritt.

G1( ):

Feld der $f_{i}$-Werte am aktuellen Startpunkt.

N:

Anzahl $n$ der Gleichungen des Dgl.ssystems.

X:

Abszissenwert des Startpunktes.

H:

Schrittweite des aktuellen Runge-Kutta-Schrittes.

OUTPUT-Parameter:

YOUT( ):

Runge-Kutta-Näherungswerte $\hat y_{i}$ an der Stelle X+H.

DERIVS:

Dieses Programm, das von allen drei Programmen dieses Systems aufgerufen wird, wird vom Benutzer erstellt und enthält die Definition der $f_{i}$-Funktionen (z. B. in C):

void derivs(double x, double y[], double f[])
{
  f[1]= .....;  // entspricht f_{1}(x,y1,y2,...)
  f[2]= .....;  // entspricht f_{2}(x,y1,y2,...)
   .
   .
  f[n]= .....;  // entspricht f_{n}(x,y1,y2,...)
}

=16cm Struktogramm 26ODEINT(YSTART,N,X1,X2,EPS,HANF,HMIN,NSTMAX,
NWERTE,XX,YY)TINY:=1.0E-30
X:=X1
XX(1):=X
H:=HANFI=1(1)NY(I):=YSTART(I)
YY(I,1):=Y(I)NSTP=1(1)NSTMAX-1 DERIVS(X,Y,F)I=1(1)N YSCAL(I):=$\vert$Y(I)$\vert$ + $\vert$F(I)*H$\vert$ + TINY X+H $>$ X2H:=X2-X...... RKQC(Y,F,N,X,H,EPS,YSCAL,HNEXT) XX(NSTP+1):=XI=1(1)NYY(I,NSTP+1):=Y(I) X $\geq$ X2I=1(1)NYSTART(I):=Y(I)NWERTE:=NSTP+1
(return)......$\vert$HNEXT$\vert$ $<$ HMINprint: 'Schrittweite kleiner HMIN'
(pause)H:=HNEXTprint:'ODEINT: mehr als NSTMAX Stuetzpunkte'
NWERTE:=NSTMAX
(return)

Struktogramm 27 RKQC(Y,F,N,X,HTRY,EPS,YSCAL,HNEXT) SAFETY:=0.9
ERRCON:=0.0006
XSAV:=XI=1(1)NYSAV(I):=Y(I)
FSAV(I):=F(I) H:=HTRY
STEPOK:=FALSE HH:=H/2.0 RK4(YSAV,FSAV,N,XSAV,HH,YTEMP) X:=XSAV+HHDERIVS(X,YTEMP,F)RK4(YTEMP,F,N,X,HH,Y) X:=XSAV+HX = XSAVprint: 'RKQC: Schrittweite zu klein.'
(pause)...... RK4(YSAV,FSAV,N,XSAV,YTEMP) ERRMAX:=0.0I=1(1)NERRV(I):=Y(I)-YTEMP(I)
TEMP:=$\vert$ ERRV(I)/YSCAL(I)$\vert$ERRMAX $<$ TEMPERRMAX:=TEMP......ERRMAX $>$ EPSH:=SAFETY*H* EXP(-0.25*LOG(ERRMAX/EPS))STEPOK:=TRUEERRMAX/EPS $<$ ERRCONHNEXT:=4*HHNEXT:=SAFETY*H* EXP(-0.2*LOG(ERRMAX/EPS))I=1(1)N Y(I):=Y(I)+ERRV(I)/15.0 (s. Kommentar S. 247)STEPOK(return)

Struktogramm 28 RK4(Y,G1,N,X,H,YOUT)I=1(1)NYT(I):=Y(I)+H/2.0*G1(I)XTEMP:=X+H/2.0DERIVS(XTEMP,YT,G2)I=1(1)NYT(I):=Y(I)+H/2.0*G2(I)DERIVS(XTEMP,YT,G3)I=1(1)NYT(I):=Y(I)+H*G3(I)XTEMP:=X+HDERIVS(XTEMP,YT,G4)I=1(1)NYOUT(I):=Y(I)+H/6.0*(G1(I)+2*(G2(I)+G3(I))+G4(I))

Anwendung von ODEINT+RKQC+RK4 auf das 'Satelliten-Problem'.

Das eben erläuterte Programm-System soll nun auf das 'Satelliten-Testproblem' angewendet werden. Das dem Dgl.ssystem (8.22) entsprechende Unterprogramm DERIVS hat z.B. in C die Form

void derivs(float x, float y[], float f[])
{
  f[1]=y[3];
  f[2]=y[4];
  f[3]=y[1]*y[4]*y[4] -alpha/y[1]/y[1];   // alpha GLOBAL = gamma*M  
                                          //              = 1966.390
  f[4]=-2.0*y[3]*y[4]/y[1];
}

Die Ergebnisse dieses Tests sind in der Abb.8.6 zusammengefaßt, umd zwar wird in dieser Abbildung die (analytisch berechnete) exakte Bahnellipse mit Runge-Kutta-Ergebnissen verglichen, die mittels eines Programmes ohne (RUKUTEST) bzw. mit Schrittweitensteuerung (ODEINT+RKQC+RK4) berechnet wurden.

Abbildung 8.6: Effizienz der Schrittweitensteuerung beim 'Satelliten-Problem'. Vergleich der exakten elliptischen Bahnkurve (volle Linie) mit numerischen Werten (Sterne). Oben: Runge-Kutta ohne Schrittweiten-Steuerung, unten: Runge-Kutta mit Schrittweiten-Steuerung.

Die Ergebnisse:

• Programm ohne Schrittweitensteuerung (Abb.8.6 oben):

  Bei diesem Testlauf wurde als konstante Schrittweite 1/50 der Umlaufzeit genommen. Diese Konstanz von $h$ im Zeitraum hat folgende Konsequenz: Da bekanntlich ein Satellit sich umso langsamer bewegt, je entfernter er von der Erde ist (2. Kepler'sches Gesetz), haben die Stützpunkte im Ortsraum gerade dort die größte Dichte, wo der Satellit die kleinste Bahngeschwindigkeit hat. Dort aber, wo diese Geschwindigkeit am größten ist (und sich am stärksten ändert), nämlich im Bereich, wo der Satellit der Erde am nächsten kommt, ist die Punktdichte am kleinsten. Gerade in diesem Bereich sollte sie aber im Interesse eines kleinen Verfahrensfehlers möglichst groß sein!

  Die Folge dieser völlig unangepaßten Stützpunktverteilung ist im Diagramm links deutlich zu sehen: Man erkennt sehr große Differenzen zwischen der exakten und der numerisch ermittelten Bahnkurve.

• Programm mit Schrittweitensteuerung, EPS=0.0001 (Abb.8.6 unten):

  In diesem Fall hat die Punktdichte genau dort ein Maximum, wo es numerisch am sinnvollsten ist (also im Bereich des kleinsten Satellit-Erde-Abstandes). Der Effekt ist evident: Bei einer ungefähr gleichen Gesamtzahl von Stützpunkten ist (zumindest grafisch) kein Unterschied zwischen der analytischen und der numerischen Bahnkurve zu erkennen!

Das Runge-Kutta-Fehlberg-Verfahren.

Die im Abschnitt (8.4.5) beschriebene Fehleranschätzung und Schrittweiten-Steuerung im vorgestellten Runge-Kutta-Programm ist zwar sehr effektiv, verbraucht aber viel Rechenzeit, denn es laufen ja zwei unabhängige Runge-Kutta-Prozesse nebeneinander.

Ebenso effektiv, aber deutlich sparsamer bzgl. der Rechenzeit ist die folgende Variante der Schrittweiten-Steuerung, die auf Fehlberg zurückgeht. Die dazu nötigen Formeln werden im folgenden wieder für den einfachen Fall eines Differentialgleichungs'systems' der Ordnung 1 erläutert^8.3:

Ein Rechenschritt von $x_0$ nach $x_0+h$ mittels eines Runge-Kutta-Verfahrens der Ordnung $p$ ergibt

$$\hat y^{(p)}(x_0+h) = y_{exakt} + C h^{p+1} .$$ (8.29)

Dieselbe Rechnung mittels einer Runge-Kutta-Formel der nächsthöheren Ordnung $p+1$ führt zu

$$\hat y^{(p+1)}(x_0+h) = y_{exakt} + \tilde C h^{p+2} .$$ (8.30)

Die Differenz von (8.29) und (8.30)

$$\hat y^{(p)}(x_0+h)-\hat y^{(p+1)}(x_0+h) = Ch^{p+1}-\tilde C h^{p+2} \approx C h^{p+1}\quad\mbox{f\uml ur kleine $h$}$$

kann nach $C$ aufgelöst werden:

$$C = \frac{\hat y^{(p)}(x_0+h)-\hat y^{(p+1)}(x_0+h)}{h^{p+1}} .$$ (8.31)

Mit diesem Näherungswert für $C$ kann der Fehler für den Runge-Kutta Schritt der Ordnung $p$ (8.29) abgeschätzt werden. Daraus kann man nun jene (ideale) Schrittweite $h_{ideal}$ berechnen, die eine vorgegebene Fehlerschranke $\epsilon$ gerade nicht überschreitet:

$$\epsilon = C h_{ideal}^{p+1} = \left(\frac{h_{ideal}}{h}\right)^{p+1} \vert\hat y^{(p)}-\hat y^{(p+1)}\vert$$

bzw.

$$h_{ideal} = h\left(\frac{\vert\hat y^{(p)}(x_0+h)-\hat y^{(p+1)}(x_0+h)\vert} {\epsilon}\right)^{-1/(p+1)} .$$ (8.32)

Vergleichen Sie dieses Ergebnis mit Glg. (8.28).

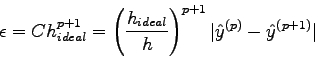
Damit ist die Vorgangsweise beim Runge-Kutta-Fehlberg-Verfahren klar: man berechnet für den Schritt $x_0\rightarrow x_0+h$ die Näherungswerte $\hat y^{(p)}(x_0+h)$ und $\hat y^{(p+1)}(x_0+h)$. Daraus bestimmt man mittels (8.32) die 'ideale' Schrittweite. Nun gibt es zwei Möglichkeiten:

1. wenn $h_{ideal} < h\quad\rightarrow$    Schritt von $x_0$ nach $x_0+h$ wird mit $h_{ideal}$ wiederholt,
2. wenn $h_{ideal} \geq h\quad\rightarrow$    der nächste Schritt wird mit $h_{ideal}$ durchgeführt.

Wo liegt nun gegenüber der Vorgangsweise in Abschnitt 8.4.5 der Vorteil? Wie Sie aus der Runge-Kutta-Theorie wissen, gibt es zu jeder Ordnung $p>1$ unendlich viele im Prinzip gleichwertige Runge-Kutta-Formeln. Fehlberg hat es nun geschafft, das folgende Formelsystem zu finden:

$$f_0=f(x_0,y_0) ,$$

$$f_1=f(x_0+\frac{h}{4}, y_0+\frac{h}{4} f_0) ,$$

$$f_2=f(x_0+\frac{3h}{8}, y_0+\frac{3h}{32} f_0+\frac{9h}{32} f_1) ,$$

$$f_3=f(x_0+\frac{12h}{13}, y_0+\frac{1932h}{2197} f_0 -\frac{7200h}{2197} f_1 + \frac{7296h}{2197} f_2) ,$$

$$f_4=f(x_0+h, y_0+\frac{439h}{216} f_0 -8h f_1 + \frac{3680h}{513} f_2-\frac{845h}{4104} f_3) ,$$

$$f_5=f(x_0+\frac{h}{2}, y_0-\frac{8h}{27} f_0 +2h f_1 - \fr... ...h}{2565} f_2+\frac{1859h}{4104} f_3 - \frac{11h}{40} f_4) .$$

Mit diesen Definitionen kann sowohl eine Runge-Kutta-Formel vierter Ordnung gebildet werden, nämlich

$$\hat y^{(4)}= y_0 + h\left( \frac{25}{216} f_0 +\frac{1408}{2565} f_2 +\frac{2197}{4104} f_3 - \frac{1}{5} f_4\right)$$

als auch eine Runge-Kutta-Formel fünfter Ordnung, nämlich

$$\hat y^{(5)}= y_0 + h\left( \frac{16}{135} f_0 +\frac{6656... ...}{56430} f_3 - \frac{9}{50} f_4 + \frac{2}{55} f_5\right) .$$

Damit ergibt sich sofort für den Fehler der Ausdruck

$$\hat y^{(4)}(x_0+h)- \hat y^{(5)}(x_0+h) = -h\left( \frac... ...}{75240} f_3 + \frac{1}{50} f_4 + \frac{2}{55} f_5\right) ,$$

und die Berechnung der idealen neuen Schrittweite erfolgt für $p$=4 gemäß (8.32) durch

$$h_{ideal} = h\left(\frac{\vert\hat y^{(4)}(x_0+h)-\hat y^{(5)}(x_0+h)\vert} {\epsilon}\right)^{-1/5} .$$ (8.33)

Weitere Verfahren zur numerischen Behandlung von Anfangswertproblemen.

Dem letzten Abschnitt dieses Kapitels sei ein ganz im saloppen Stil amerikanischer Publikationen gehaltener Absatz aus den 'Numerical Recipes' [9] vorangestellt:

For many scientific users, forth-order Runge-Kutta is not just the first word on ODE integrators, but the last word as well. In fact, you can get pretty far on this old workhorse, especially if you combine it with an adaptive stepsize algorithm ... Keep in mind, however, that the old workhorse's last trip may well be to take you to the poorhouse: Bulirsch-Stoer or predictor-corrector methods can be very much more efficient for problems where very high accuracy is a requirement. Those methods are the high-strung racehorses. Runge-Kutta is for ploughing the fields.

In der Tat sind die hier im Detail vorgestellten Verfahren (Runge-Kutta und Runge-Kutta-Fehlberg) nicht der Weisheit allerletzter Schluß, wenn es um die numerische Behandlung von Anfangswertproblemen geht. Dennoch erschien es dem Autor dieses Skriptums besser, ein klassisches Verfahren (auch wenn es ein alter Ackergaul ist) in einem sehr robusten und brauchbaren Programm vorzustellen, als die manchmal (nicht immer!) überlegenen 'Rennpferde' (Bulirsch-Stoer-Methode und predictor-corrector-Methode). Für ein an sich wünschenswertes 'Sowohl-Als auch' ist jedoch der hier gesteckte Rahmen einfach zu knapp.

Ich muß daher (nicht zum ersten Mal in diesem Skriptum) an die Eigeninitiative der an numerischen Verfahren interessierten Hörer appellieren und gebe im folgenden nur eine kleine Literaturliste:

• Näherungsweise Lösung gewöhnlicher Differentialgleichungen: [19], S.127-228 (ausführliche Theorie).
• Ordinary Differential Equations: [7], S.360-414 (wie immer sehr zu empfehlen: Theorie, numerische Probleme, Vergleich von Methoden usw.).
• Prädiktor-Korrektor-Verfahren nach Adams-Bashford-Moulton: [2], S.220ff (Theorie), S.428ff (Programm).
• Extrapolationsverfahren nach Bulirsch-Stoer: [2], S.233ff (Theorie), S.434ff (Programm).
• Richardson Extrapolation and the Bulirsch-Stoer Method: [9], S.563ff (kurze Beschreibung und Programme).
• Predictor-Corrector Methods: [9], S.569ff (kurze Beschreibung).
• Prädiktor-Korrektor-Verfahren nach Adams: [13], S.288f (Theorie), S.290f (Algol-Programm).
• Natürlich hat jede professionelle numerisch-mathematische Library eine Reihe von einschlägigen Programmen (s. Abschnitt 8.7).

Steife Systeme von Differentialgleichungen

Noch einige Anmerkungen zu sog. stiff sets of differential equations, die in der Praxis immer wieder vorkommen. Es handelt sich dabei um Systeme, deren Lösungsfunktionen aus Termen bestehen, die extrem verschiedene Abhängigkeits-Empfindlichkeiten von der unabhängigen Variablen haben.
Am einfachsten ist dies durch ein Beispiel zu erläutern (aus [10], S. 734):

Angenommen, es soll das System

$$y'_{1}(x) = 998 y_{1} + 1998 y_{2}$$

$$y'_{2}(x) = -999 y_{1} + 1999 y_{2}$$

mit den Anfangsbedingungen $y_{1}(0)=1$ und $y_{2}(0)=0$ gelöst werden.

Die exakte Lösung dieses Problems lautet

$$y_{1}(x) = 2 {\rm e}^{-x} - {\rm e}^{-1000x}\qquad\mbox{and}\qquad y_{2}(x) = -{\rm e}^{-x} + {\rm e}^{-1000x} .$$ (8.34)

Es zeigt sich, daß die numerische Berechnung solcher Probleme mit konventionellen Methoden (z. B. mit Runge-Kutta) zu einer Instabilität des Verfahrens führt, wenn man nicht mit extrem kleinen Schrittweiten [im konkreten Fall mit $h«1/1000$ (!)] arbeitet. Dies, obwohl die zweiten Terme in (8.34) bereits für sehr kleine $x$ praktisch auf Null abgeklungen sind und die danach die Lösungen simple $\exp(-x)$-Funktionen darstellen.

Für solche Probleme gibt es spezielle Lösungsverfahren, wie zum Beispiel die Methode von Kaps und Rentrop^8.4. Entsprechende C-Programme mit theoretischen Erläuterungen finden Sie in [10], S. 734ff.

Mehr zum Thema 'Numerische Behandlung von Anfangswertproblemen' können Sie in meiner Lehrveranstaltung im SS Ausgewählte Kapitel aus
'Numerische Methoden in der Physik' erfahren.
Stichworte: Methode von Bulirsch und Stör; predictor-corrector-Methode; steife Systeme usw.

Software-Angebot

NAG:

    Die folgende Tabelle gibt einen Überblick über das Angebot dieser Library in bezug auf Cauchy-Probleme. Verwendet wird primär die Runge-Kutta-Methode (Programme d02puf und d02pcf). Bei Problemen mit großem Integrationsbereich und hohen Genauigkeitsansprüchen kommt die Methode nach Adams zum Einsatz (Programme d02cjf und andere). Als drittes Verfahren wird die BDF-Methode (Backward Differentiation Formula) angeboten; diese Methode hat sich vor allem bei stiff equations (s. Abschnitt 8.7.1) bewährt.

ODEPACK (in www.netlib.org):

    (p.d.) Paket mit F77-Programmen für Anfangswertprobleme gewöhnlicher Differentialgleichungen, sowohl für nicht-steife (predictor-corrector-Methode von Adams) als auch für steife Systeme (backward differentiation formula von Gear).

toms-504.f (in www.netlib.org):

    Public domain Programm 'GERK' von H. A. Watts und L. F. Shampine: Fehlberg fourth (fifth) order Runge-Kutta method with global error assessment to solve a system of differential equations. Beschreibung der Parameter im Programmlisting.

Numerical Recipes:

    In diesen Büchern finden Sie eine Reihe von ODE-Programmen^8.5 in F77, F90 und C:

odeint+rkqs+rkck             Runge-Kutta-Fehlberg-Methode
odeint+bsstep+mmid+pzextr    Bulirsch-Stoer-Methode
stiff+jacobn+ludcmp+lubksb   stiff differential systems

Eine Beschreibung dieser Programme bzw. Testprogramme finden Sie in [9], [10] sowie auf Ihrem PC im Computerraum in den Verzeichnissen

/usr/local/numeric/numrec/c  (oder fortran-77 oder fortran-90)

Numerical Algorithms with C or FORTRAN

    In diesem Werk werden ebenfalls etliche ODE-Programme(F77/F90/C) angeboten. Die Parameter bzw. abhängigen Unterprogramme werden in den Listings beschrieben. Hier eine Auswahl:

rk_fehl.c           Runge-Kutta-Fehlberg-Methode
bulirsch.c          Bulirsch-Stoer-Gregg-Methode
ab_mou.c            Praediktor-Korrektor-Verfahren von
                    Adams-Bashforth-Moulton
gear.c              Verfahren von Gear fuer steife Dgl.en

(inkl. verschiedene Header-Dateien)

rktrb.f90  plus dependencies    Runge-Kutta-Methoden
frkfsy.f90 plus dependencies    Runge-Kutta-Fehlberg-Methode
hull.f90   plus dependencies    Runge-Kutta-Hull-Methode
irkdrv.f90 plus dependencies    Implicite Runge-Kutta-Methoden
gear4.f90  plus dependencies    stiff differential equations

Alle diese Programme finden Sie in den Verzeichnissen
/usr/local/numeric/num_alg/c/ansic/ansic/17   ('17' bedeutet: Kap. 17)         
/usr/local/numeric/num_alg/f77/f90/kap17

MATLAB.6:

    Dieses Programmsystem bietet ebenfalls eine grosse Auswahl von ODE-Programmen an; Infos darüber s. das MATLAB function reference. Das Standardprogramm für non-stiff systems heißt ode45, für stiff systems gibt es ode15s.
Eine ausführliche Beschreibung des jeweiligen Matlab-Programms inkl. Testbeispiel und Programm-Listing erhalten Sie durch Eingabe der folgenden Befehle (z. B.) im Matlab-Fenster:

    more on
    type ode45
    more off

Wer mehr über dieses Thema wissen möchte, beschaffe sich das folgende Buch:
D. Arnold and J. C. Polking, Ordinary Differential Equations Using Matlab, Prentice Hall 1999.